
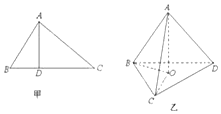
 如图甲,在△ABC中,AB⊥AC,AD⊥BC,D为.垂足,则AB2=BD•BC,该结论称为射影定理.如图乙,在三棱锥A-BCD中,AD⊥平面ABC,AO⊥平面BCD,O为垂足,且O在△BCD内,类比射影定理,探究S△ABC、S△BCO、S△BCD这三者之间满足的关是S△ABC2=S△BCO•S△BCD.
如图甲,在△ABC中,AB⊥AC,AD⊥BC,D为.垂足,则AB2=BD•BC,该结论称为射影定理.如图乙,在三棱锥A-BCD中,AD⊥平面ABC,AO⊥平面BCD,O为垂足,且O在△BCD内,类比射影定理,探究S△ABC、S△BCO、S△BCD这三者之间满足的关是S△ABC2=S△BCO•S△BCD. 分析 这是一个类比推理的题,在由平面图形到空间图形的类比推理中,一般是由点的性质类比推理到线的性质,由线的性质类比推理到面的性质,由已知在平面几何中,(如图所示)若△ABC中,AB⊥AC,AD⊥BC,D是垂足,则AB2=BD•BC,我们可以类比这一性质,推理出若三棱锥A-BCD中,AD⊥面ABC,AO⊥面BCD,O为垂足,则S△ABC2=S△BCO•S△BCD.
解答 解:由已知在平面几何中,
若△ABC中,AB⊥AC,AD⊥BC,D是垂足,则AB2=BD•BC,
我们可以类比这一性质,推理出:
若三棱锥A-BCD中,AD⊥面ABC,AO⊥面BCD,O为垂足,
则S△ABC2=S△BCO•S△BCD.
故答案为S△ABC2=S△BCO•S△BCD.
点评 类比推理的一般步骤是:(1)找出两类事物之间的相似性或一致性;(2)用一类事物的性质去推测另一类事物的性质,得出一个明确的命题(猜想).


 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | MP<OM<0 | B. | OM>0>MP | C. | OM<MP<0 | D. | MP>0>OM |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | Χ2越大,“X与Y有关系”可信程度越小 | |
| B. | Χ2越小,“X与Y有关系”可信程度越小 | |
| C. | Χ2越接近0,“X与Y无关”程度越小 | |
| D. | Χ2越大,“X与Y无关”程度越大 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | k=-6 | B. | k=6 | C. | k=$\frac{1}{2}$ | D. | k=-1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com