
分析 利用设[x]表示不超过x的最大整数,依次化简个根式,然后利用裂项相消法即可得结论.
解答 解:由题意,[x]表示不超过x的最大整数,设n为正整数,则$n<\sqrt{n({n+1})}<n+1$,于是,$[{\sqrt{n({n+1})}}]=n$,
∴$\frac{1}{{[\sqrt{n×(n+1)}]×[\sqrt{(n+1)×(n+2)}]×[\sqrt{(n+2)×(n+3)}]}}=\frac{1}{n×(n+1)×(n+2)}=\frac{1}{2}(\frac{1}{n×(n+1)}-\frac{1}{(n+1)×(n+2)})$,
∴原式=$\frac{1}{2}(\frac{1}{1×2}-\frac{1}{2×3}+\frac{1}{2×3}-\frac{1}{3×4}+…+\frac{1}{n×(n+1)}-\frac{1}{(n+1)×(n+2)})$
=$\frac{1}{4}-\frac{1}{2(n+1)×(n+2)}$.
点评 本题考查了对定义的理解和裂项相消法的计算.属于中档题.


 备战中考寒假系列答案
备战中考寒假系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{2}}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{\sqrt{3}}{3}$ | D. | $\frac{3}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | $\frac{\sqrt{10}}{10}$ | C. | $\frac{2\sqrt{10}}{10}$ | D. | $\frac{3\sqrt{10}}{10}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
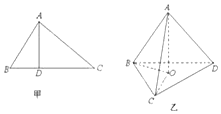 如图甲,在△ABC中,AB⊥AC,AD⊥BC,D为.垂足,则AB2=BD•BC,该结论称为射影定理.如图乙,在三棱锥A-BCD中,AD⊥平面ABC,AO⊥平面BCD,O为垂足,且O在△BCD内,类比射影定理,探究S△ABC、S△BCO、S△BCD这三者之间满足的关是S△ABC2=S△BCO•S△BCD.
如图甲,在△ABC中,AB⊥AC,AD⊥BC,D为.垂足,则AB2=BD•BC,该结论称为射影定理.如图乙,在三棱锥A-BCD中,AD⊥平面ABC,AO⊥平面BCD,O为垂足,且O在△BCD内,类比射影定理,探究S△ABC、S△BCO、S△BCD这三者之间满足的关是S△ABC2=S△BCO•S△BCD.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com