练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】化简求值：
    （1）sin（﹣1320°）cos1110°+cos（﹣1020°）sin750°
    （2） ．

    【答案】
    （1）

    解：sin（﹣1320°）cos1110°+cos（﹣1020°）sin750°

    =sin（4×360°﹣1320°）cos（1110°﹣3×360°）+cos（3×360°﹣1020°）sin（750°﹣2×360°）

    =sin120°cos30°+cos60°sin30°

    =sin60°cos30°+cos60°sin30°

    =sin（60°+30°）

    =1


    （2）

    解：

    =

    =﹣1


    【解析】（1）由条件利用诱导公式、两角和的正弦公式，化简所给式子的值，可得结果．（2）利用诱导公式化简所给式子的值，可得结果．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知直线l经过点P（﹣2，5），且斜率为﹣
    （1）求直线l的方程；
    （2）若直线m与l平行，且点P到直线m的距离为3，求直线m的方程．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某商场拟对某商品进行促销，现有两种方案供选择，每种促销方案都需分两个月实施，且每种方案中第一个月与第二个月的销售相互独立.根据以往促销的统计数据，若实施方案1，预计第一个月的销量是促销前的1.2倍和1.5倍的概率分别是0.6和0.4，第二个月的销量是第一个月的1.4倍和1.6倍的概率都是0.5；若实施方案2，预计第一个月的销量是促销前的1.4倍和1.5倍的概率分别是0.7和0.3，第二个月的销量是第一个月的1.2倍和1.6倍的概率分别是0.6和0.4.令表示实施方案的第二个月的销量是促销前销量的倍数.

    （Ⅰ）求， 的分布列；

    （Ⅱ）不管实施哪种方案， 与第二个月的利润之间的关系如下表，试比较哪种方案第二个月的利润更大.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】将圆为参数)上的每一点的横坐标保持不变，纵坐标变为原来的倍，得到曲线

    (1)求出的普通方程；

    (2)设直线： 与的交点为， ，以坐标原点为极点， 轴正半轴为极轴建立极坐标系，求过线段的中点且与垂直的直线的极坐标方程.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】电视传媒公司为了了解某地区电视观众对某类体育节目的收视情况，随机抽取了100名观众进行调查，下面是根据调查结果绘制的观众日均收看该体育节目时间的频率分布直方

    图：

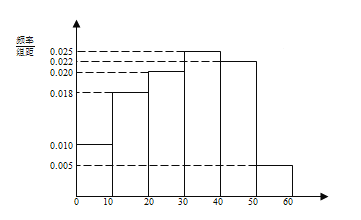
    将日均收看该体育节目时间不低于40分钟的观众称为“体育迷”.

    （Ⅰ）根据已知条件完成下面的列联表，并据此资料，在犯错误的概率不超过的前提下，你是否有理由认为“体育迷”与性别有关？


    非体育迷

    体育迷

    合计

    男




    女


    10

    55

    合计




    （Ⅱ）将上述调查所得到的频率视为概率，现在从该地区大量电视观众中，采用随机抽样方法每次抽取1名观众，抽取3次，记被抽取的3名观众中的“体育迷”人数为.若每次抽取的结果是相互独立的，求的分布列，期望和方差.

    附：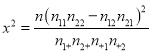







    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】雾霾天气对城市环境造成很大影响，按照国家环保部发布的标准：居民区的PM2.5（大气中直径小于或等于2.5微米的颗粒物）年平均浓度不得超过35微克/立方米.某市环保部门加强了对空气质量的监测，抽取某居民区监测点的20天PM2.5的24小时平均浓度的监测数据，制成茎叶图，如图：

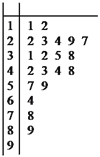
    （Ⅰ）完成如下频率分布表，并在所给的坐标系中画出的频率分布直方图；

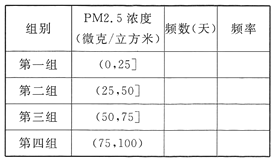
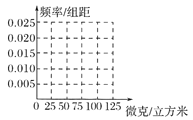
    （Ⅱ）从样本中PM2.5的24小时平均浓度超过50微克/立方米的天数中，随机抽取2天，求恰好有一天PM2.5的24小时平均浓度超过75微克/立方米的概率.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某省高考改革新方案，不分文理科，高考成绩实行“”的构成模式，第一个“3”是语文、数学、外语，每门满分150分，第二个“3”由考生在思想政治、历史、地理、物理、化学、生物6个科目中自主选择其中3个科目参加等级性考试，每门满分100分，高考录取成绩卷面总分满分750分.为了调查学生对物理、化学、生物的选考情况，将“某市某一届学生在物理、化学、生物三个科目中至少选考一科的学生”记作学生群体，从学生群体中随机抽取了50名学生进行调查，他们选考物理，化学，生物的科目数及人数统计如下表：

    (I)从所调查的50名学生中任选2名，求他们选考物理、化学、生物科目数量不相等的概率；

    (II)从所调查的50名学生中任选2名，记表示这2名学生选考物理、化学、生物的科目数量之差的绝对值，求随机变量的分布列和数学期望；

    (III)将频率视为概率，现从学生群体中随机抽取4名学生，记其中恰好选考物理、化学、生物中的两科目的学生数记作，求事件“”的概率.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某单位招聘职工分为笔试和面试两个环节，将笔试成绩合格（满分100分，及格60分，精确到个位数）的应聘者进行统计，得到如下的频率分布表：

    分组

    频数

    频率

    [60，70]

    0.16

    （70，80]

    22

    （80，90]

    14

    0.28

    （90，100]

    合计

    50

    1

    （Ⅰ）确定表中的值（直接写出结果，不必写过程）

    （Ⅱ）面试规定，笔试成绩在80分（不含80分）以上者可以进入面试环节，面试时又要分两关，首先面试官依次提出4个问题供选手回答，并规定，答对2道题就终止回答，通过第一关可以进入下一关，如果前三题均没有答对，则不再回答第四题并且不能进入下一关，假定某选手获得面试资格的概率与答对每道题的概率相等.

    求该选手答完3道题而通过第一关的概率；

    记该选手在面试第一关中的答题个数为X，求X的分布列及数学期望.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在直三棱柱ABC—A1B1C1中，AB=BC=BB1， ，D为AC上的点，B1C∥平面A1BD；

    （1）求证：BD⊥平面；

    （2）若且，求三棱锥A-BCB1的体积．

    查看答案和解析>>

    同步练习册答案