
【题目】某单位招聘职工分为笔试和面试两个环节,将笔试成绩合格(满分100分,及格60分,精确到个位数)的应聘者进行统计,得到如下的频率分布表:
分组 | 频数 | 频率 |
[60,70] |
| 0.16 |
(70,80] | 22 |
|
(80,90] | 14 | 0.28 |
(90,100] |
|
|
合计 | 50 | 1 |
(Ⅰ)确定表中![]() 的值(直接写出结果,不必写过程)
的值(直接写出结果,不必写过程)
(Ⅱ)面试规定,笔试成绩在80分(不含80分)以上者可以进入面试环节,面试时又要分两关,首先面试官依次提出4个问题供选手回答,并规定,答对2道题就终止回答,通过第一关可以进入下一关,如果前三题均没有答对,则不再回答第四题并且不能进入下一关,假定某选手获得面试资格的概率与答对每道题的概率相等.
![]() 求该选手答完3道题而通过第一关的概率;
求该选手答完3道题而通过第一关的概率;
![]() 记该选手在面试第一关中的答题个数为X,求X的分布列及数学期望.
记该选手在面试第一关中的答题个数为X,求X的分布列及数学期望.
【答案】(Ⅰ)![]() (Ⅱ)见解析;
(Ⅱ)见解析; ![]()
【解析】【试题分析】(1)借助频率、频数、样本容量之间的关系![]() 进行求解;(2)先依据题设中答题的要求,运用互斥事件和对立事件的概率计算公式进行分析求解;(3)先求出随机变量
进行求解;(2)先依据题设中答题的要求,运用互斥事件和对立事件的概率计算公式进行分析求解;(3)先求出随机变量![]() 的值进行分类
的值进行分类![]() ,分别求出其概率
,分别求出其概率![]() ,
, ![]() ,
, ![]() ,列出概率分布表,再运用随机变量的数学期望公式计算求解:
,列出概率分布表,再运用随机变量的数学期望公式计算求解:
解:(I)由频率分布表可得a=8,b=6,x=0.44,y=0.12
(II)由频率分布表及(I)的结论可知,该选手能进入面试的概率即答对每道题的概率为0.28+0.12=0.4.记“答对第i道题”为事件Ai,i=1,2,3,4,则P(Ai)=0.4
![]() 记“该选手答完3道题而通过第一关”为事件A,
记“该选手答完3道题而通过第一关”为事件A,
则![]() =0.192
=0.192
![]() 随机变量X的可能取值为2,3,4.
随机变量X的可能取值为2,3,4.
![]()
![]()
![]()
故X的分布列为
X | 2 | 3 | 4 |
P | 0.16 | 0.408 | 0.432 |
所以![]() .
.


科目:高中数学 来源: 题型:
【题目】研究人员随机调查统计了某地1000名“上班族”每天在工作之余使用手机上网的时间,并将其绘制为如图所示的频率分布直方图.若同一组数据用该区间的中点值作代表,则可估计该地“上班族”每天在工作之余使用手机上网的平均时间是( ) 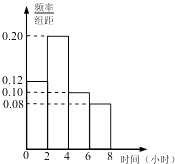
A.1.78小时
B.2.24小时
C.3.56小时
D.4.32小时
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}满足:an≠0,a1= ![]() ,an﹣an+1=2anan+1 . (n∈N*).
,an﹣an+1=2anan+1 . (n∈N*).
(1)求证:{ ![]() }是等差数列,并求出an;
}是等差数列,并求出an;
(2)证明:a1a2+a2a3+…+anan+1< ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】△ABC中,角A,B,C的对边分别为a,b,c,且cosC= ![]() .
.
(1)求角B的大小;
(2)若BD为AC边上的中线,cosA= ![]() ,BD=
,BD= ![]() ,求△ABC的面积.
,求△ABC的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C: ![]() =1(a>b>0)的一个长轴顶点为A(2,0),离心率为
=1(a>b>0)的一个长轴顶点为A(2,0),离心率为 ![]() ,直线y=k(x﹣1)与椭圆C交于不同的两点M,N,
,直线y=k(x﹣1)与椭圆C交于不同的两点M,N,
(Ⅰ)求椭圆C的方程;
(Ⅱ)当△AMN的面积为 ![]() 时,求k的值.
时,求k的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的右焦点
的右焦点![]() ,椭圆
,椭圆![]() 的左,右顶点分别为
的左,右顶点分别为![]() .过点
.过点![]() 的直线
的直线![]() 与椭圆交于
与椭圆交于![]() 两点,且
两点,且![]() 的面积是
的面积是![]() 的面积的3倍.
的面积的3倍.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)若![]() 与
与![]() 轴垂直,
轴垂直,![]() 是椭圆
是椭圆![]() 上位于直线
上位于直线![]() 两侧的动点,且满足
两侧的动点,且满足![]() ,试问直线
,试问直线![]() 的斜率是否为定值,请说明理由.
的斜率是否为定值,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,椭圆
中,椭圆![]() :
:![]() 的离心率为
的离心率为![]() ,直线
,直线![]() 被椭圆
被椭圆![]() 截得的线段长为
截得的线段长为![]() .
.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)过原点的直线与椭圆![]() 交于
交于![]() ,
,![]() 两点(
两点(![]() ,
,![]() 不是椭圆
不是椭圆![]() 的顶点),点
的顶点),点![]() 在椭圆
在椭圆![]() 上,且
上,且![]() .直线
.直线![]() 与
与![]() 轴、
轴、![]() 轴分别交于
轴分别交于![]() ,
,![]() 两点.设直线
两点.设直线![]() ,
,![]() 的斜率分别为
的斜率分别为![]() ,
,![]() ,证明存在常数
,证明存在常数![]() 使得
使得![]() ,并求出
,并求出![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com