
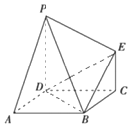
 如图,四边形ABCD为正方形,PD⊥平面ABCD,CE⊥平面ABCD,CE=AB,PD=λCE(λ>1)
如图,四边形ABCD为正方形,PD⊥平面ABCD,CE⊥平面ABCD,CE=AB,PD=λCE(λ>1)分析 (1)证明:AD⊥平面PDCE,即可证明PE⊥AD;
(2)分别求出体积,利用VB-CDE:V多面体ABDEP=1:4,求λ的值.
解答 (1)证明:∵ABCD是正方形,∴AD⊥CD,
∵PD⊥平面ABCD,∴AD⊥PD,
∵PD∩CD=D,
∴AD⊥平面PDCE,
∵PD?平面PDCE,
∴PE⊥AD
(2)解:设AB=a,则AD=CE=a,VB-CDE=$\frac{1}{3}×(\frac{1}{2}{a}^{2})×a$=$\frac{1}{6}{a}^{3}$,
V多面体ABDEP=VB-PDE+VP-ABD=$\frac{1}{3}×(\frac{1}{2}λ{a}^{2})×a+\frac{1}{3}×\frac{1}{2}{a}^{2}×λa$=$\frac{1}{3}λ{a}^{3}$,
∵VB-CDE:V多面体ABDEP=1:4,∴λ=2.
点评 本题考查线面垂直的判定与性质,考查体积的计算,考查学生分析解决问题的能力,属于中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y2=2x | B. | y2=3x | C. | y2=4x | D. | y2=6x |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
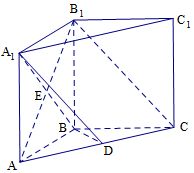 如图,在直三棱柱ABC-A1B1C1中,AB=BC=BB1,AB1∩A1B=E,D为AC上的点,B1C∥平面A1BD;
如图,在直三棱柱ABC-A1B1C1中,AB=BC=BB1,AB1∩A1B=E,D为AC上的点,B1C∥平面A1BD;查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
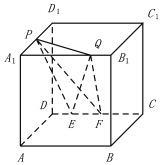 如图,在棱长为a的正方体ABCD-A1B1C1D1中,P为A1D1的中点,Q为A1B1上任意一点,E,F为CD上任意两点,且EF的长为定值,则下面的四个值中不为定值的是( )
如图,在棱长为a的正方体ABCD-A1B1C1D1中,P为A1D1的中点,Q为A1B1上任意一点,E,F为CD上任意两点,且EF的长为定值,则下面的四个值中不为定值的是( )| A. | 点Q到平面PEF的距离 | B. | 直线PE与平面QEF所成的角 | ||
| C. | 三棱锥P-QEF的体积 | D. | 二面角P-EF-Q的大小 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{\sqrt{2}}}{2}$ | B. | $\frac{{3\sqrt{2}}}{2}$ | C. | $\sqrt{2}$ | D. | $3\sqrt{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com