
| A. | y2=2x | B. | y2=3x | C. | y2=4x | D. | y2=6x |
分析 分别过A、B作准线的垂线,利用抛物线定义将A、B到焦点的距离转化为到准线的距离,结合已知比例关系,即可得p值,进而可得方程
解答 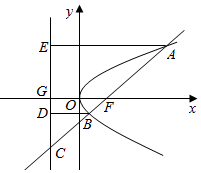 解:分别过点A,B作准线的垂线,分别交准线于点E,D,
解:分别过点A,B作准线的垂线,分别交准线于点E,D,
设|BF|=a,则|BC|=3a,|BD|=a,∴$\frac{DB}{BC}=\frac{1}{3}$,
在直角三角形ACE中,∵|AF|=3,|AC|=3+4a,
∴3|AE|=|AC|
∴3+4a=9,即a=$\frac{3}{2}$,
∵BD∥FG,∴$\frac{DB}{FG}=\frac{BC}{FC}$,$\frac{a}{p}=\frac{3a}{4a}=\frac{3}{4}$,解得p=2,
从而抛物线的方程为y2=4x.
故选:C.
点评 本题考查抛物线的定义及其应用,抛物线的几何性质,过焦点的弦的弦长关系,转化化归的思想方法,属中档题.


 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案科目:高中数学 来源: 题型:选择题
| A. | y=sinx | B. | y=cosx | C. | y=tanx | D. | y=-tanx |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (10,7) | B. | (10,5) | C. | (-4,-3) | D. | (-4,-1) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
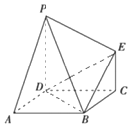 如图,四边形ABCD为正方形,PD⊥平面ABCD,CE⊥平面ABCD,CE=AB,PD=λCE(λ>1)
如图,四边形ABCD为正方形,PD⊥平面ABCD,CE⊥平面ABCD,CE=AB,PD=λCE(λ>1)查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | p或q为假,p且q为假,非p为真 | B. | p或q为真,p且q为假,非 p为真 | ||
| C. | p或q为假,p且q为假,非p为假 | D. | p或q为真,p且q为假,非p为假 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com