
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
科目:高中数学 来源: 题型:解答题
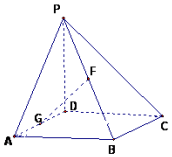 如图,在四棱锥P-ABCD中,PD⊥底面ABCD,底面ABCD为正方形,PD=DC=2,G,F分别是AD,PB的中点.
如图,在四棱锥P-ABCD中,PD⊥底面ABCD,底面ABCD为正方形,PD=DC=2,G,F分别是AD,PB的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
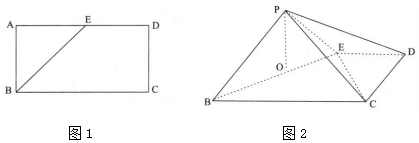
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y2=2x | B. | y2=3x | C. | y2=4x | D. | y2=6x |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
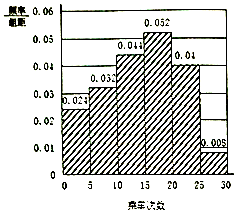 沪昆高速铁路全线2016年12月28日开通运营.途经鹰潭北站的G1421、G1503两列列车乘务组工作人员为了了解乘坐本次列车的乘客每月需求情况,分别在两个车次各随机抽取了100名旅客进行调查,下面是根据调查结果,绘制了月乘车次数的频率分布直方图和频数分布表.
沪昆高速铁路全线2016年12月28日开通运营.途经鹰潭北站的G1421、G1503两列列车乘务组工作人员为了了解乘坐本次列车的乘客每月需求情况,分别在两个车次各随机抽取了100名旅客进行调查,下面是根据调查结果,绘制了月乘车次数的频率分布直方图和频数分布表.| 乘车次数分组 | 频数 |
| [0,5) | 15 |
| [5,10) | 20 |
| [10,15) | 25 |
| [15,20) | 24 |
| [20,25) | 11 |
| [25,0] | 5 |
| 老乘客 | 新乘客 | 合计 | |
| 50岁以上 | |||
| 50岁以下 | |||
| 合计 |
| P(k2≥k0) | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 |
| k0 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com