
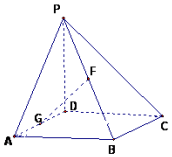
 如图,在四棱锥P-ABCD中,PD⊥底面ABCD,底面ABCD为正方形,PD=DC=2,G,F分别是AD,PB的中点.
如图,在四棱锥P-ABCD中,PD⊥底面ABCD,底面ABCD为正方形,PD=DC=2,G,F分别是AD,PB的中点.分析 (I)以D为原点建立空间直角坐标系,利用$\overrightarrow{PA}$•$\overrightarrow{DC}$=0,证得PA⊥CD;
(Ⅱ)利用$\overrightarrow{FG}$•$\overrightarrow{CB}$=0,$\overrightarrow{FG}$•$\overrightarrow{PC}$=0,去证GF⊥平面PCB.
解答 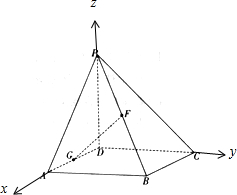 证明:(I)以D为原点建立空间直角坐标系则A(2,0,0)B(2,2,0)C(0,2,0)P(0,0,2)F(1,1,1)
证明:(I)以D为原点建立空间直角坐标系则A(2,0,0)B(2,2,0)C(0,2,0)P(0,0,2)F(1,1,1)
$\overrightarrow{PA}$=(2,0,-2),$\overrightarrow{DC}$=(0,2,0),
∴$\overrightarrow{PA}$•$\overrightarrow{DC}$=0,∴$\overrightarrow{PA}$⊥$\overrightarrow{DC}$,
∴PA⊥CD;
(Ⅱ)设G(1,0,0)则$\overrightarrow{FG}$=(0,-1,-1),$\overrightarrow{CB}$=(2,0,0),$\overrightarrow{PC}$=(0,2,-2)
∴$\overrightarrow{FG}$•$\overrightarrow{CB}$=0,$\overrightarrow{FG}$•$\overrightarrow{PC}$=0,
∴FG⊥CB,FG⊥PC,
∵CB∩PC=C,
∴GF⊥平面PCB.
点评 本题考查线面、面面位置关系的证明.借助于空间向量的运算,降低了思维难度,增加了解题方法.


科目:高中数学 来源: 题型:选择题
| A. | $[\frac{π}{6},\frac{π}{2}]$ | B. | $[\frac{π}{4},\frac{π}{3}]$ | C. | $[\frac{π}{3},\frac{π}{2}]$ | D. | $[\frac{π}{6},\frac{π}{4}]$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $(-3,\frac{3}{2})$ | B. | $(-∞,-3)∪(\frac{3}{2},+∞)$ | C. | $(-∞,-1)∪(\frac{3}{2},+∞)$ | D. | $(-∞,-1)∪(1,\frac{3}{2})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
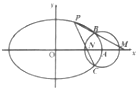 已知椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$的长轴长为4,焦距为$2\sqrt{3}$,以A为圆心的圆(x-2)2+y2=r2(r>0)与椭圆相交于B、C两点.
已知椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$的长轴长为4,焦距为$2\sqrt{3}$,以A为圆心的圆(x-2)2+y2=r2(r>0)与椭圆相交于B、C两点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=sinx | B. | y=cosx | C. | y=tanx | D. | y=-tanx |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com