
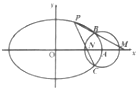
 ��֪��Բ$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1��{a��b��0}��$�ij��᳤Ϊ4������Ϊ$2\sqrt{3}$����AΪԲ�ĵ�Բ��x-2��2+y2=r2��r��0������Բ�ཻ��B��C���㣮
��֪��Բ$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1��{a��b��0}��$�ij��᳤Ϊ4������Ϊ$2\sqrt{3}$����AΪԲ�ĵ�Բ��x-2��2+y2=r2��r��0������Բ�ཻ��B��C���㣮���� ������Բ$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1��{a��b��0}��$�ij��᳤�����࣬��a2=b2+c2�����a��b���ɣ�
������B��x0��y0����C��x0��-y0�����ɵ�$\overrightarrow{AB}•\overrightarrow{AC}={��{x_0}-2��^2}-y_0^2$=${��{x_0}-2��^2}-��1-\frac{x_0^2}{4}��$=$\frac{5}{4}x_0^2-4{x_0}+3=\frac{5}{4}{��{x_0}-\frac{8}{5}��^2}-\frac{1}{5}$����-2��x0��2�����$\overrightarrow{AB}•\overrightarrow{AC}$��ȡֵ��Χ��
������P��x1��y1����y1�١�y0�����õ�ֱ��PB��PC�ķ��̣��ֱ���y=0��${x_M}=\frac{{{x_1}{y_0}-{x_0}{y_1}}}{{{y_0}-{y_1}}}$��${x_N}=\frac{{{x_1}{y_0}+{x_0}{y_1}}}{{{y_0}+{y_1}}}$����${S_{��POM}}•{S_{��PON}}=\frac{1}{4}|OM||ON|•y_1^2$=$\frac{1}{4}|{x_M}{x_N}|•y_1^2=y_1^2$��
����-1��y1��1�����S��POM•S��PONȡ�����ֵ��
��� �⣺������Բ$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1��{a��b��0}��$�ij��᳤Ϊ4������Ϊ$2\sqrt{3}$����2a=4��2c=2$\sqrt{3}$��
��a=2��b2=a2-c2=1
����Բ�ı�����Ϊ$\frac{x^2}{4}+{y^2}=1$��
������B��x0��y0����C��x0��-y0����$\frac{x_0^2}{4}+y_0^2=1$��
��$\overrightarrow{AB}•\overrightarrow{AC}={��{x_0}-2��^2}-y_0^2$=${��{x_0}-2��^2}-��1-\frac{x_0^2}{4}��$=$\frac{5}{4}x_0^2-4{x_0}+3=\frac{5}{4}{��{x_0}-\frac{8}{5}��^2}-\frac{1}{5}$��
��Ϊ-2��x0��2������$\overrightarrow{AB}•\overrightarrow{AC}$��ȡֵ��ΧΪ$[-\frac{1}{5}��16��$��
������P��x1��y1����y1�١�y0������$\frac{x_1^2}{4}+y_1^2=1$��
ֱ��PB��PC�ķ��̷ֱ�Ϊ��$PB��y-{y_1}=\frac{{{y_0}-{y_1}}}{{{x_0}-{x_1}}}��x-{x_1}��$��$PC��y-{y_1}=\frac{{-{y_0}-{y_1}}}{{{x_0}-{x_1}}}��x-{x_1}��$��
�ֱ���y=0��${x_M}=\frac{{{x_1}{y_0}-{x_0}{y_1}}}{{{y_0}-{y_1}}}$��${x_N}=\frac{{{x_1}{y_0}+{x_0}{y_1}}}{{{y_0}+{y_1}}}$��
����${x_M}{x_N}=\frac{x_1^2y_0^2-x_0^2y_1^2}{y_0^2-y_1^2}$=$\frac{��4-4y_1^2��y_0^2-��4-4y_0^2��y_1^2}{y_0^2-y_1^2}$=$\frac{4��y_0^2-y_1^2��}{y_0^2-y_1^2}=4$��
����${S_{��POM}}•{S_{��PON}}=\frac{1}{4}|OM||ON|•y_1^2$=$\frac{1}{4}|{x_M}{x_N}|•y_1^2=y_1^2$��
��Ϊ-1��y1��1������S��POM•S��PONȡ�����ֵΪ1��
���� ���⿼������Բ�ķ��̣�ֱ������Բ��λ�ù�ϵ��������������������ķ�Χ�������е��⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��-�ޣ�0�� | B�� | ��0��$\frac{1}{2e}$�� | C�� | ��-�ޣ�0���ȣ�$\frac{1}{2e}$��+�ޣ� | D�� | ��$\frac{1}{2e}$��+�ޣ� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��-2��0�� | B�� | ��0��2�� | C�� | ��-1��2�� | D�� | ��-2��-1�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | {2} | B�� | {3} | C�� | {5��6} | D�� | {3��5��6} |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
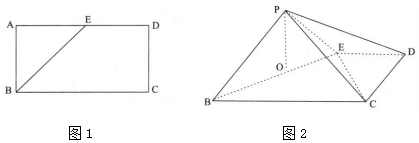
 ��ͼ����һ�������������ε�ֱ�������������ǣ��������ⳤΪ1dm��dmΪ���ף�����Ϊ5dm������С��������Ե����������ϣ��ҵ��µ������ֱ�Ϊ3dm��4dm����ˮ����©����£���������װ��ˮ���Ϊ��������
��ͼ����һ�������������ε�ֱ�������������ǣ��������ⳤΪ1dm��dmΪ���ף�����Ϊ5dm������С��������Ե����������ϣ��ҵ��µ������ֱ�Ϊ3dm��4dm����ˮ����©����£���������װ��ˮ���Ϊ��������| A�� | $\frac{9}{2}d{m^3}$ | B�� | 4dm3 | C�� | $\frac{7}{2}d{m^3}$ | D�� | 3dm3 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
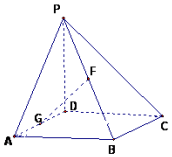 ��ͼ��������P-ABCD�У�PD�͵���ABCD������ABCDΪ�����Σ�PD=DC=2��G��F�ֱ���AD��PB���е㣮
��ͼ��������P-ABCD�У�PD�͵���ABCD������ABCDΪ�����Σ�PD=DC=2��G��F�ֱ���AD��PB���е㣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com