Question

5．已知椭圆E：$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1（{a＞b＞0}）$的左、右焦点分别为F₁，F₂，左、右顶点分别为A，B．以F₁F₂为直径的圆O过椭圆E的上顶点D，直线DB与圆O相交得到的弦长为$\frac{{2\sqrt{3}}}{3}$．设点P（a，t）（t≠0），连接PA交椭圆于点C，坐标原点为O．
（I）求椭圆E的方程；
（II）若三角形ABC的面积不大于四边形OBPC的面积，求|t|的最小值．

Answer 1

分析 （Ⅰ）由题意可知：b=c，则$a=\sqrt{2}b$，则直线DB的方程为$y=-\frac{{\sqrt{2}}}{2}x+b$，由题意可知$2\sqrt{{b^2}-{{（\frac{b}{{\sqrt{1+\frac{1}{2}}}}）}^2}}=\frac{{2\sqrt{3}}}{3}$，即可求得b及a的值，求得椭圆方程；
（2）设直线PA的方程为$y=\frac{t}{{2\sqrt{2}}}（x+\sqrt{2}）$，代入椭圆方程，求得C点坐标，直线BC的斜率为${k_{BC}}=-\frac{{\sqrt{2}}}{t}$，由于直线OP的斜率为${k_{OP}}=\frac{t}{{\sqrt{2}}}$，可得OP⊥BC，分别求得三角形ABC的面积及四边形OBPC的面积由$\frac{{4\sqrt{2}|t|}}{{4+{t^2}}}≤\frac{{\sqrt{2}|{{t^3}+2t}|}}{{4+{t^2}}}$，即可求得丨t丨取值范围，即可求得|t|的最小值．

解答 解：（Ⅰ）因为以F₁，F₂为直径的圆O过点D，所以b=c，则圆O的方程为x²+y²=b²，
又a²=b²+c²，所以$a=\sqrt{2}b$，直线DB的方程为$y=-\frac{{\sqrt{2}}}{2}x+b$，直线DB与圆O相交得到的弦长为$\frac{{2\sqrt{3}}}{3}$，
则$2\sqrt{{b^2}-{{（\frac{b}{{\sqrt{1+\frac{1}{2}}}}）}^2}}=\frac{{2\sqrt{3}}}{3}$，所以b=1，$a=\sqrt{2}$，
所以椭圆E的方程为        $\frac{x^2}{2}+{y^2}=1$．…（5分）
（Ⅱ）由已知得：$a=\sqrt{2}$，b=1，椭圆方程为$\frac{x^2}{2}+{y^2}=1$，
设直线PA的方程为$y=\frac{t}{{2\sqrt{2}}}（x+\sqrt{2}）$，由$\left\{\begin{array}{l}\frac{x^2}{2}+{y^2}=1\\ y=\frac{t}{{2\sqrt{2}}}（x+\sqrt{2}）\end{array}\right.$
整理得$（4+{t^2}）{x^2}+2\sqrt{2}{t^2}x+2{t^2}-8=0$，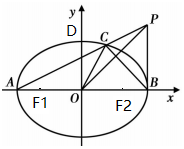
解得：${x_1}=-\sqrt{2}$，${x_2}=\frac{{4\sqrt{2}-\sqrt{2}{t^2}}}{{4+{t^2}}}$，则点C的坐标是$（\frac{{4\sqrt{2}-\sqrt{2}{t^2}}}{{4+{t^2}}}，\frac{4t}{{4+{t^2}}}）$，
故直线BC的斜率为${k_{BC}}=-\frac{{\sqrt{2}}}{t}$，由于直线OP的斜率为${k_{OP}}=\frac{t}{{\sqrt{2}}}$，
所以k_BC•k_OP=-1，所以OP⊥BC．…（10分）
所以${S_{OBPC}}=\frac{1}{2}×|{OP}|×|{BC}|=\frac{{\sqrt{2}|{{t^3}+2t}|}}{{4+{t^2}}}$，${S_{△ABC}}=\frac{1}{2}×2\sqrt{2}×\frac{4|t|}{{4+{t^2}}}=\frac{{4\sqrt{2}|t|}}{{4+{t^2}}}$，所以$\frac{{4\sqrt{2}|t|}}{{4+{t^2}}}≤\frac{{\sqrt{2}|{{t^3}+2t}|}}{{4+{t^2}}}$，
整理得2+t²≥4，$|t|≥\sqrt{2}$，所以${|t|_{min}}=\sqrt{2}$．…（13分）

点评 本题考查椭圆的标准方程，直线与椭圆的位置位置关系，考查直线的斜率公式，考查计算能力，属于中档题．