
分析 (1)由已知利用三角形面积公式,同角三角函数基本关系式及余弦定理化简$tanA=\sqrt{3}$,结合A的范围利用特殊角的三角函数值即可得解A的值.
(2)由A的值,利用三角函数恒等变换的应用即可化简得解.
解答 (本题满分为12分)
解:(1)因为:$4S=\sqrt{3}({b^2}+{c^2}-{a^2})$,
所以:$4•\frac{1}{2}bcsinA=\sqrt{3}•2bccosA$,即$tanA=\sqrt{3}$,
因为:A∈(0,180°),
所以A=60°.…(6分)
(2)$原式=sin{70°}({1-\sqrt{3}tan{{50}°}})=sin{70°}•\frac{{cos{{50}°}-\sqrt{3}sin{{50}°}}}{{cos{{50}°}}}$…(8分)
=$sin{70°}•\frac{{-2sin{{20}°}}}{{cos{{50}°}}}=cos{20°}•\frac{{-2sin{{20}°}}}{{sin{{40}°}}}=-\frac{{sin{{40}°}}}{{sin{{40}°}}}=-1$.…(12分)
点评 本题主要考查了三角形面积公式,同角三角函数基本关系式及余弦定理,特殊角的三角函数值,三角函数恒等变换的应用在解三角形中的综合应用,考查了转化思想,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{500}{3}π$ | B. | $\frac{125}{6}π$ | C. | 100π | D. | 25π |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 样本数据中x=0时,一定有$y=\hat a$ | |
| B. | x增加一个单位时,y平均增加$\hat b$个单位 | |
| C. | 样本数据中x=0时,可能有$y=\hat a$ | |
| D. | 直线必经过点$(\overline x,\overline y)$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
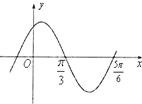 函数f(x)=sin(ωx+φ)(ω>0,|φ|<$\frac{π}{2}$)的图象如图所示,为了得到函数y=cos(2x+$\frac{π}{6}$)的图象,只需将y=f(x)的图象( )
函数f(x)=sin(ωx+φ)(ω>0,|φ|<$\frac{π}{2}$)的图象如图所示,为了得到函数y=cos(2x+$\frac{π}{6}$)的图象,只需将y=f(x)的图象( )| A. | 向左平移$\frac{π}{3}$个单位长度 | B. | 向右平移$\frac{π}{3}$个单位长度 | ||
| C. | 向左平移$\frac{π}{6}$个单位长度 | D. | 向右平移$\frac{π}{6}$个单位长度 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com