
| A. | $\frac{{\sqrt{5}-1}}{2}$ | B. | -2 | C. | $\frac{{\sqrt{5}+1}}{2}$ | D. | 4 |
分析 设f(x)=max{x2+x-2,2x},由定义讨论当x2+x-2≥2x,当x2+x-2<2x,求得f(x),运用二次函数和一次函数的单调性,可得最小值.
解答 解:设f(x)=max{x2+x-2,2x},
当x2+x-2≥2x,即x≥2或x≤-1时,f(x)=x2+x-2,
由于对称轴x=-$\frac{1}{2}$,可得f(x)在x≥2递增,可得f(x)≥f(2)=4,
f(x)在x≤-1递减,可得f(x)≥f(-1)=-2;
当x2+x-2<2x,即-1<x<2时,f(x)=2x,
可得f(x)在-1<x<2递增,即有-2<f(x)<4,
综上可得,f(x)的值域为[-2,+∞),
即有f(x)=max{x2+x-2,2x}的最小值为-2.
故选B.
点评 本题考查新定义的理解和运用,考查二次不等式的解法,考查二次函数和一次函数的最值的求法,属于中档题.


科目:高中数学 来源: 题型:解答题
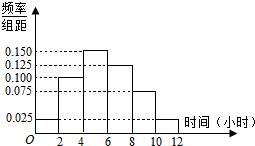 某校共有学生1600人,其中男生1000人,女生600人.为调查该校学生每周平均体育运动时间的情况,采用分层抽样的方法,收集40位学生每周平均体育运动时间的样本数据(单位:小时).
某校共有学生1600人,其中男生1000人,女生600人.为调查该校学生每周平均体育运动时间的情况,采用分层抽样的方法,收集40位学生每周平均体育运动时间的样本数据(单位:小时).查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 中位数>平均数>众数 | B. | 众数>中位数>平均数 | ||
| C. | 众数>平均数>中位数 | D. | 平均数>众数>中位数 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,-2)∪[1,+∞) | B. | (-∞,-2) | C. | (-2,1] | D. | [1,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ∅ | B. | $\left\{{x\left|{x=\frac{1}{5}}\right.}\right\}$ | C. | $\left\{{x\left|{x≠\frac{1}{5}}\right.}\right\}$ | D. | $\left\{{x\left|{x≤\frac{1}{5}}\right.}\right\}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com