练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    10．执行如图所示的程序框图，若输出的S=183，则判断框内应填入的条件是（　　）
    A．k＞7？B．k＞6？C．k＞5？D．k＞4？

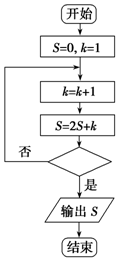
    分析 分析程序中各变量、各语句的作用，再根据流程图所示的顺序，可知：该程序的作用是累加并输入S的值，条件框内的语句是决定是否结束循环，模拟执行程序即可得到答案．

    解答 解：程序在运行过程中各变量值变化如下表：
                k   S    是否继续循环
    循环前 1   0
    第一圈 2   2         是
    第二圈 3   7         是
    第三圈 4   18        是
    第四圈 5   41        是
    第五圈 6   88        是
    第六圈 7   183       否
    故退出循环的条件应为k＞6？
    故选：B．

    点评 算法是新课程中的新增加的内容，也必然是新高考中的一个热点，应高度重视．程序填空也是重要的考试题型，这种题考试的重点有：①分支的条件②循环的条件③变量的赋值④变量的输出．其中前两点考试的概率更大．此种题型的易忽略点是：不能准确理解流程图的含义而导致错误．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：填空题

    20．函数f（x）=$\frac{x}{x-1}$（x≥3）的最大值为$\frac{3}{2}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    1．函数f（x）=x+$\frac{4}{x-3}$，x∈（3，+∞）的最小值为（　　）
    A．3B．4C．6D．7

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    18．在正项数列{an}中，a1=2，且点（$\sqrt{a_n}$，$\sqrt{{a_{n-1}}}$）在直线x-$\sqrt{2}$y=0上，则前n项和Sn等于（　　）
    A．2n-1B．2n+1-2C．${2^{\frac{n}{2}}}-\sqrt{2}$D．${2^{\frac{n-2}{2}}}-\sqrt{2}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    5．已知a，b，c分别为△ABC三个内角A，B，C的对边，且满足2bcosC=2a-c．
    （Ⅰ）求B；            
    （Ⅱ）若△ABC的面积为$\sqrt{3}$，b=2求a，c的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    15．对甲、乙两名同学的学习成绩进行抽样分析，各抽5门功课，得到的观测值如表：
    甲8090857090
    乙80100709080
    问：（1）甲、乙的平均成绩谁较好？
    （2）谁的各门功课发展较平衡？

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    2．已知钝角α满足cosα=-$\frac{3}{5}$，则tan（α+$\frac{π}{4}$）的值为$-\frac{1}{7}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    19．将函数$f（x）=3sin（{2x+\frac{π}{3}}）$的图象向右平移$\frac{π}{2}$个单位长度，所得图象对应的函数（　　）
    A．其中一条对称轴方程为$x=-\frac{π}{6}$B．在区间$[{\frac{π}{12}，\frac{7π}{12}}]$上单调递增
    C．当$x=\frac{π}{12}+kπ（{k∈Z}）$时取得最大值D．在区间$[{-\frac{π}{6}，\frac{π}{3}}]$上单调递增

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    20．设函数f（x）=（x2-8x+c1）（x2-8x+c2）（x2-8x+c3）（x2-8x+c4），集合M={x|f（x）=0}={x1，x2，x3，…，x7}⊆N*，设c1≥c2≥c3≥c4则c1-c4=（　　）
    A．11B．13C．7D．9

    查看答案和解析>>

    同步练习册答案