
| A. | 若a=0,则y=f(x)与y=3是同一函数 | |
| B. | 若0<a≤1,则$f(-\frac{π}{2})<f(2-{log_3}2)<f[{(\frac{1}{3})^{{{log}_3}\frac{2}{3}}}]<f({log_3}5)<f(\frac{π}{2})$ | |
| C. | 若a=2,则对任意使得f(m)=0的实数m,都有f(-m)=1 | |
| D. | 若a>3,则f(cos2)<f(cos3) |
分析 A,若a=0,则y=f(x)的定义域为{x|x≠0},y=3定义域为R,不是同一函数;
B,若0<a≤1时,可得函数f(x)在[-$\frac{π}{2}$,$\frac{π}{2}$]上为增函数,即可判断;
C,a=2时,f(x)=$\frac{1}{{2}^{x}+1}+asinx$,f(x)+f(-x)=$\frac{1}{{2}^{x}+1}+asinx+\frac{1}{{2}^{-x}+1}+asin(-x)$=$\frac{1}{{2}^{x}+1}+\frac{1}{{z}^{-x}+1}=1$,即可判定;
D,当a>3时,f(x)在[-$\frac{π}{2}$,$\frac{π}{2}$]上为增函数,且cos2>cos3,即可判定.
解答 解:对于A,若a=0,则y=f(x)的定义域为{x|x≠0},y=3定义域为R,不是同一函数,故错;
对于B,若0<a≤1时,可得函数f(x)在[-$\frac{π}{2}$,$\frac{π}{2}$]上为增函数,∵$(\frac{1}{3})^{lo{{g}_{3}}^{\frac{2}{3}}}$=$\frac{3}{2}=lo{g}_{3}\sqrt{27}>lo{g}_{3}5$,故错;
对于C,a=2时,f(x)=$\frac{1}{{2}^{x}+1}+asinx$,f(x)+f(-x)=$\frac{1}{{2}^{x}+1}+asinx+\frac{1}{{2}^{-x}+1}+asin(-x)$=$\frac{1}{{2}^{x}+1}+\frac{1}{{z}^{-x}+1}=1$,∴则对任意使得f(m)=0的实数m,都有f(-m)=1,正确;
对于D,当a>3时,f(x)在[-$\frac{π}{2}$,$\frac{π}{2}$]上为增函数,且cos2>cos3,则f(cos2)>f(cos3),故错.
故选:C
点评 本题考查了命题真假的判定,涉及到函数的性质,属于基础题.


科目:高中数学 来源: 题型:填空题
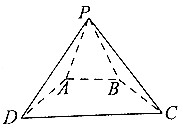 已知四棱锥P-ABCD中,底面四边形ABCD为等腰梯形,且AB∥CD,AB=$\frac{1}{2}$CD,PA=PB=AD,PA+AD=CD=4$\sqrt{3}$,若平面PAB⊥平面ABCD,则四棱锥P-ABCD外接球的表面积为52π.
已知四棱锥P-ABCD中,底面四边形ABCD为等腰梯形,且AB∥CD,AB=$\frac{1}{2}$CD,PA=PB=AD,PA+AD=CD=4$\sqrt{3}$,若平面PAB⊥平面ABCD,则四棱锥P-ABCD外接球的表面积为52π.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
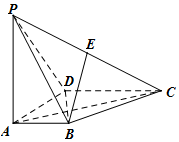 如图,在四棱锥P-ABCD中,PA⊥底面ABCD,AD⊥AB,AB∥DC,AD=DC=AP=2,AB=1,点E为棱PC的中点.
如图,在四棱锥P-ABCD中,PA⊥底面ABCD,AD⊥AB,AB∥DC,AD=DC=AP=2,AB=1,点E为棱PC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
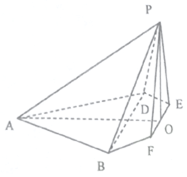 在边长为4的菱形ABCD中,∠DAB=60°,点E,F分别是边CD,CB的中点,AC∩EF=O,沿EF将△CEF翻折到△PEF,连接PA,PB,PD,得到如图的五棱锥,且$PB=\sqrt{10}$.
在边长为4的菱形ABCD中,∠DAB=60°,点E,F分别是边CD,CB的中点,AC∩EF=O,沿EF将△CEF翻折到△PEF,连接PA,PB,PD,得到如图的五棱锥,且$PB=\sqrt{10}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{2}$ | B. | -$\sqrt{2}$ | C. | 0 | D. | $\frac{\sqrt{2}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 男生 | 女生 | 合计 | |
| 收看 | 10 | ||
| 不收看 | 8 | ||
| 合计 | 30 |
| P(K2>k0) | 0.100 | 0.050 | 0.010 |
| k0 | 2.706 | 3.841 | 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com