
如图,四棱锥P﹣ABCD的底面ABCD为直角梯形,AD//BC,且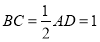 ,BC⊥DC,∠BAD=60°,平面PAD⊥底面ABCD,E为AD的中点,△PAD为等边三角形,M是棱PC上的一点,设
,BC⊥DC,∠BAD=60°,平面PAD⊥底面ABCD,E为AD的中点,△PAD为等边三角形,M是棱PC上的一点,设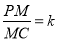 (M与C不重合).
(M与C不重合).
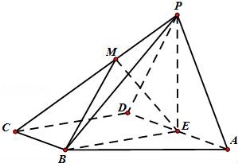
(1)求证:CD⊥DP;
(2)若PA∥平面BME,求k的值;
(3)若二面角M﹣BE﹣A的平面角为150°,求k的值.
科目:高中数学 来源:2017届河北武邑中学高三上学期第一次调研数学(文)试卷(解析版) 题型:选择题
根据统计资料,我国能源生产自1992年以来发展很快,下面是我国能源生产总量(折合亿吨标准煤)的几个统计数据:1992年8.6亿吨,5年后的1997年10.4亿吨,10年后的2002年12.9亿吨.有关专家预测,到2007年我国能源生产总量将达到17.1亿吨,则专家是依据下列哪一类函数作为数学模型进行预测的( )
A.一次函数 B.二次函数 C.指数函数 D.对数函数
查看答案和解析>>
科目:高中数学 来源:2016届天津市高三一模考试数学(理)试卷(解析版) 题型:填空题
在平面直角坐标系中,以坐标原点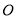 为极点,
为极点,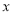 轴的正半轴为极轴建立极坐标系.已知直线
轴的正半轴为极轴建立极坐标系.已知直线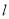 的极坐标方程为
的极坐标方程为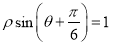 ,圆
,圆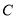 的参数方程为
的参数方程为 (
(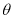 为参数).求直线
为参数).求直线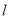 与圆
与圆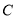 相交所得弦长为 .
相交所得弦长为 .
查看答案和解析>>
科目:高中数学 来源:2016-2017学年湖北襄阳五中高二上开学考数学(理)试卷(解析版) 题型:填空题
设直线系M:xcosθ+(y﹣2)sinθ=1(0≤θ≤2π),对于下列四个命题:
A.M中所有直线均经过一个定点
B.存在定点P不在M中的任一条直线上
C.对于任意整数n(n≥3),存在正n边形,其所有边均在M中的直线上
D.M中的直线所能围成的正三角形面积都相等
其中真命题的代号是 (写出所有真命题的代号).
查看答案和解析>>
科目:高中数学 来源:2016-2017学年湖北襄阳五中高二上开学考数学(理)试卷(解析版) 题型:选择题
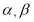 是两个平面,
是两个平面,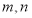 是两条直线,有下列四个命题:
是两条直线,有下列四个命题:
①如果 ,那么
,那么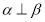 .
.
②如果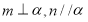 ,那么
,那么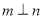 .
.
③如果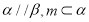 ,那么
,那么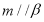 .
.
④如果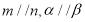 ,那么
,那么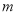 与
与 所成的角和
所成的角和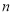 与
与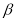 所成的角相等.
所成的角相等.
其中正确的命题为( )
A.②③④ B.①②④ C.①③④ D.①②④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com