
已知曲线 的参数方程是
的参数方程是 (φ为参数),以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,曲线
(φ为参数),以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,曲线 的极坐标方程是ρ=2,正方形ABCD的顶点都在
的极坐标方程是ρ=2,正方形ABCD的顶点都在 上,且A,B,C,D依逆时针次序排列,点A的极坐标为
上,且A,B,C,D依逆时针次序排列,点A的极坐标为 .
.
(Ⅰ)求点A,B,C,D的直角坐标;
(Ⅱ)设P为 上任意一点,求
上任意一点,求 的取值范围.
的取值范围.
(Ⅰ)A(1,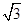 ),B(-
),B(-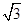 ,1),C(-1,-
,1),C(-1,-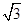 ),D(
),D(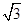 ,-1);(Ⅱ)
,-1);(Ⅱ) 的取值范围是[32,52]
的取值范围是[32,52]
解析试题分析:(Ⅰ)根据已知条件可得A(2cos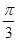 ,2sin
,2sin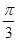 ),B(2cos(
),B(2cos(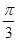 +
+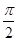 ),2sin(
),2sin(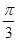 +
+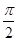 )),C(2cos(
)),C(2cos(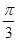 +π),2sin(
+π),2sin(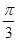 +π)),D(2cos(
+π)),D(2cos(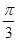 +
+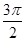 ),2sin(
),2sin(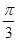 +
+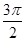 )),然后将其化为直角坐标即可;(Ⅱ)设P(2cosφ,3sinφ),令S=
)),然后将其化为直角坐标即可;(Ⅱ)设P(2cosφ,3sinφ),令S= ,利用三角函数求解.
,利用三角函数求解.
试题解析: (1)由已知可得A(2cos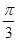 ,2sin
,2sin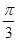 ),B(2cos(
),B(2cos(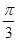 +
+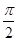 ),2sin(
),2sin(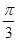 +
+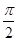 )),
)),
C(2cos(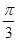 +π),2sin(
+π),2sin(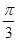 +π)),D(2cos(
+π)),D(2cos(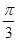 +
+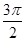 ),2sin(
),2sin(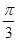 +
+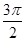 )),4分
)),4分
即A(1,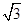 ),B(-
),B(-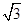 ,1),C(-1,-
,1),C(-1,-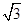 ),D(
),D(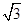 ,-1). 5分
,-1). 5分
(2)设P(2cosφ,3sinφ),令S= ,
,
则S=16cos2φ+36sin2φ+16=32+20sin2φ. 9分
因为0≤sin2φ≤1,所以S的取值范围是[32,52]. 10分
考点:极坐标和参数方程、三角函数、直角坐标和极坐标互化.


科目:高中数学 来源: 题型:解答题
已知直线 的参数方程为
的参数方程为 为参数),以坐标原点为极点,
为参数),以坐标原点为极点,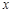 轴的正半轴为极轴建立极坐标系,圆
轴的正半轴为极轴建立极坐标系,圆 的极坐标方程为
的极坐标方程为 .
.
(1)求圆 的直角坐标方程;
的直角坐标方程;
(2)若 是直线
是直线 与圆面
与圆面 ≤
≤ 的公共点,求
的公共点,求 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知平面直角坐标系 ,以
,以 为极点,
为极点,  轴的非负半轴为极轴建立极坐标系,
轴的非负半轴为极轴建立极坐标系, 点的极坐标为
点的极坐标为 ,曲线
,曲线 的极坐标方程为
的极坐标方程为
(1)写出点 的直角坐标及曲线
的直角坐标及曲线 的直角坐标方程;
的直角坐标方程;
(2)若 为曲线
为曲线 上的动点,求
上的动点,求 中点
中点 到直线
到直线 (
( 为参数)距离的最小值.
为参数)距离的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
在直角坐标系 中,已知圆
中,已知圆 的参数方程
的参数方程 (
( 为参数),以
为参数),以 为极点,
为极点, 轴的非负半轴为极轴建立极坐标系.
轴的非负半轴为极轴建立极坐标系.
(Ⅰ)求圆 的极坐标方程;
的极坐标方程;
(Ⅱ)直线 ,射线
,射线 与圆
与圆 的交点为
的交点为 ,与直线
,与直线 的交点为
的交点为 ,求线段
,求线段 的长.
的长.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
在直角坐标系中,以原点为极点,x轴的正半轴为极轴建立极坐标系,已知曲线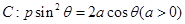 过点P(-2,-4)的直线
过点P(-2,-4)的直线 为参数)与曲线C相交于点M,N两点.
为参数)与曲线C相交于点M,N两点.
(Ⅰ)求曲线C和直线 的普通方程;
的普通方程;
(Ⅱ)若|PM|,|MN|,|PN |成等比数列,求实数a的值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
在极坐标系中,圆C的方程为ρ=2  sin
sin  ,以极点为坐标原点,极轴为x轴的正半轴建立平面直角坐标系,直线l的参数方程为
,以极点为坐标原点,极轴为x轴的正半轴建立平面直角坐标系,直线l的参数方程为 (t为参数),判断直线l和圆C的位置关系.
(t为参数),判断直线l和圆C的位置关系.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com