
分析 先将方程两边看成两个函数,再通过分类讨论并结合函数图象确定参数a的取值范围.
解答 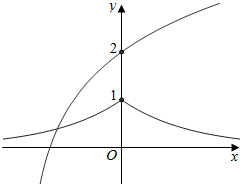 解:设y1=a|x|,y2=log2(x+2)+1,
解:设y1=a|x|,y2=log2(x+2)+1,
对a分类讨论如下:
①当a=1时,y1=1为常数函数,
与函数y2的图象只有一个交点,符合题意;
②当a>1时,y1为偶函数,图象关于y轴对称,
且x<0时,函数y1递减,x>0时,函数y1递增,
因此,函数y1与y2的图象有两个交点;
③当0<a<1时,y1为偶函数,如右图,
且x<0时,函数y1递增,x>0时,函数y1递减,
因此,函数y1与y2的图象只有一个交点;
综合以上讨论得,a∈(0,1].
故答案为:(0,1].
点评 本题主要考查了指数函数的图象和性质,以及根的存在和个数的判断,体现了分类讨论和数形结合的解题思想,属于中档题.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:填空题
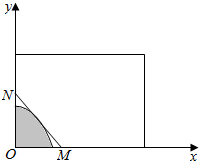 如图,某房地产公司要在一块矩形宽阔地面上开发物业,阴影部分是不能开发的古建筑群,且要求用在一条直线上的栏栅进行隔离,古建筑群的边界为曲线y=1-$\frac{4}{3}$x2的一部分,栏栅与矩形区域边界交于点M、N,则当能开发的面积达到最大时,OM的长为1.
如图,某房地产公司要在一块矩形宽阔地面上开发物业,阴影部分是不能开发的古建筑群,且要求用在一条直线上的栏栅进行隔离,古建筑群的边界为曲线y=1-$\frac{4}{3}$x2的一部分,栏栅与矩形区域边界交于点M、N,则当能开发的面积达到最大时,OM的长为1.查看答案和解析>>
科目:高中数学 来源:2017届湖南衡阳八中高三上学期月考二数学(理)试卷(解析版) 题型:选择题
已知定义在R上的奇函数f(x)的导函数为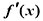 ,当x<0时,f(x)满足
,当x<0时,f(x)满足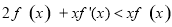 ,则f(x)在R上的零点个数为( )
,则f(x)在R上的零点个数为( )
A.1 B.3 C.5 D .1或3
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $(-\frac{1}{4},\frac{1}{4}]$ | B. | $(0,\frac{1}{4}]$ | C. | $(\frac{1}{4},\frac{1}{3}]$ | D. | $(0,\frac{1}{3})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $(\frac{3}{4},2]$ | B. | [2,3) | C. | (1,2] | D. | (-∞,-2]∪[2,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 9 | B. | 10 | C. | 11 | D. | 12 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a8=a2a4 | B. | a6=a2+a4 | C. | ${a_4}^2={a_2}{a_6}$ | D. | ${a_8}^2={a_2}{a_6}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com