
分析 令f(x)=0,可得a=$\frac{x-1}{{e}^{x}}$,令g(x)=$\frac{x-1}{{e}^{x}}$,求出函数的最大值,可得实数a的最大值.
解答 解:f(x)=aex-x+1=0,
则a=$\frac{x-1}{{e}^{x}}$,
令g(x)=$\frac{x-1}{{e}^{x}}$,则g′(x)=$\frac{2-x}{{e}^{x}}$,
∴g(x)在(-∞,2]上递增,在[2,+∞)上递减,
故当x=2时,g(x)取最大值$\frac{1}{{e}^{2}}$,
故a≤$\frac{1}{{e}^{2}}$,
即实数a的最大值是$\frac{1}{{e}^{2}}$,
故答案为:$\frac{1}{{e}^{2}}$
点评 本题考查的知识点是函数的零点,函数的值域,函数的最值,难度中档.


科目:高中数学 来源:2017届湖南衡阳八中高三上学期月考二数学(理)试卷(解析版) 题型:解答题
设函数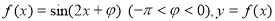 图像的一条对称轴是直线
图像的一条对称轴是直线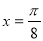 .
.
(1)求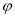 并用“五点法”画出函数
并用“五点法”画出函数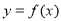 在区间
在区间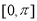 上的图像;
上的图像;
(2)求函数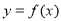 的单调增区间;
的单调增区间;
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{3}{2}$ | D. | $\frac{2}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充要条件 | B. | 充分不必要条件 | ||
| C. | 必要不充分条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com