
分析 (1)根据f(x)=log${\;}_{\frac{1}{2}}$$\frac{1-ax}{x-1}$满足f(-x)=-f(x),结合对数函数的图象和性质,可得a值;
(2)任取x1>x2>1,判断f(x1),f(x2)的大小,结合函数单调性的定义,可得f(x)在(1,+∞)内单调递增;
(3)若对于[3,4]上的每一个x的值,不等式f(x)>($\frac{1}{2}$)x+m恒成立,令g(x)=f(x)-($\frac{1}{2}$)x,则g(x)min>m,结合(2)中单调性,求出函数的最值,可得m的范围.
解答 解:(1)∵f(-x)=-f(x),
∴${log}_{\frac{1}{2}}\frac{1+ax}{-x-1}=-{log}_{\frac{1}{2}}\frac{1-ax}{x-1}$=${log}_{\frac{1}{2}}\frac{x-1}{1-ax}$,
∴$\frac{1+ax}{-x-1}$=$\frac{x-1}{1-ax}$>0,
∴1-a2x2=1-x2,
∴a=±1.
检验a=1(舍),
∴a=-1.…(4分)
证明:(2)任取x1>x2>1,
∴x1-1>x2-1>0.
∴0<$\frac{2}{x1-1}$<$\frac{2}{x2-1}$⇒1<1+$\frac{2}{x1-1}$<1+$\frac{2}{x2-1}$⇒1<$\frac{x1+1}{x1-1}$<$\frac{x2+1}{x2-1}$⇒${log}_{\frac{1}{2}}\frac{{x}_{1}+1}{{x}_{1}-1}$>${log}_{\frac{1}{2}}\frac{{x}_{2}+1}{{x}_{2}-1}$.
即f(x1)>f(x2),
∴f(x)在(1,+∞)内单调递增.…(8分)
解:(3)依题意有f(x)-($\frac{1}{2}$)x>m恒成立.
令g(x)=f(x)-($\frac{1}{2}$)x,
则g(x)min>m.…(10分)
易知g(x)在[3,4]上是增函数,
∴g(x)min=g(3)=-$\frac{9}{8}$,…(12分)
∴m<-$\frac{9}{8}$时,原不等式在[3,4]上恒成立.…(14分)
点评 本题考查的知识点是对数函数的图象和性质,熟练掌握对数函数的图象和性质是解答的关键.


 每课必练系列答案
每课必练系列答案 巧学巧练系列答案
巧学巧练系列答案科目:高中数学 来源:2017届湖南衡阳八中高三上学期月考二数学(理)试卷(解析版) 题型:选择题
已知定义在R上的奇函数f(x)的导函数为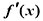 ,当x<0时,f(x)满足
,当x<0时,f(x)满足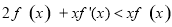 ,则f(x)在R上的零点个数为( )
,则f(x)在R上的零点个数为( )
A.1 B.3 C.5 D .1或3
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $(\frac{3}{4},2]$ | B. | [2,3) | C. | (1,2] | D. | (-∞,-2]∪[2,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 9 | B. | 10 | C. | 11 | D. | 12 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com