Question

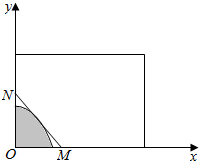
16．如图，某房地产公司要在一块矩形宽阔地面上开发物业，阴影部分是不能开发的古建筑群，且要求用在一条直线上的栏栅进行隔离，古建筑群的边界为曲线y=1-$\frac{4}{3}$x²的一部分，栏栅与矩形区域边界交于点M、N，则当能开发的面积达到最大时，OM的长为1．

Answer 1

分析 先设切点的坐标，并运用导数得出切线方程，再求出直线的横纵截距，最后运用基本不等式最最值．

解答 解：根据题意，当开发面积最大值时，三角形OMN的面积就最小，
设MN与曲线y=1-$\frac{4}{3}x^2$相切于点T（m，1-$\frac{4}{3}$m²），m∈（0，$\frac{\sqrt{3}}{2}$），
对函数线y=1-$\frac{4}{3}x^2$求导得，y'=-$\frac{8}{3}x$，
所以，切线MN的斜率k_MN=-$\frac{8}{3}m$，
直线MN的方程为：y-（1-$\frac{4}{3}$m²）=-$\frac{8}{3}m$（x-m），
令y=0得，x_M=$\frac{4m^2+3}{8m}$，令x=0得，y_N=$\frac{4m^2+3}{3}$，
S_△MON=$\frac{1}{2}$×$\frac{4m^2+3}{8m}$×$\frac{4m^2+3}{3}$
=$\frac{1}{48}$[16m³+24m+$\frac{9}{m}$]
=$\frac{1}{48}$[（16m³+$\frac{1}{m}$+$\frac{1}{m}$+$\frac{1}{m}$）+6（4m+$\frac{1}{m}$）]
≥$\frac{1}{48}$[4•$\root{4}{16}$+6•2•$\sqrt{4}$]=$\frac{32}{48}$=$\frac{2}{3}$，
当且仅当：16m³=$\frac{1}{m}$且4m=$\frac{1}{m}$，解得m=$\frac{1}{2}$，
即三角形MON面积的最小值为$\frac{2}{3}$，
此时，OM=$\frac{4m^2+3}{8m}$=1．
故答案为：1．
说明：本题也可以运用导数研究三角形MON面积的最小值．

点评 本题主要考查了基本不等式在求最值问题中的应用，构造出合理的结构使得基本不等式能同时取得最值是解决本题的关键，属于中档题．