练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    11．对满足不等式组$\left\{\begin{array}{l}{x+1≥0}\\{x+y-4≤0}\\{x-y≤0}\end{array}\right.$的任意实数x，y，z=x2+y2-4x的最小值是（　　）
    A．-2B．0C．1D．6

    分析 作出不等式组对应的平面区域，利用z的几何意义结合两点间的距离进行求解即可．

    解答 解：作出不等式组对应的平面区域如图：
    z=x2+y2-4x=（x-2）2+y2-4
    则z的几何意义为区域内的点到点D（2，0）的距离的平方-4，
    由图象知D到直线x-y=0的距离为d=$\frac{|2-0|}{\sqrt{2}}=\frac{2}{\sqrt{2}}$=$\sqrt{2}$，
    此时z取得最小值为z=d2-4=2-4=-2，
    故选：A．

    点评 本题主要考查线性规划的应用，利用z的几何意义结合点到直线的距离公式是解决本题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

    1．已知A，B，D三点不在一条直线上，且A（-2，0），B（2，0），|AD|=2，点E是BD的中点．
    （1）求E点轨迹方程；
    （2）已知椭圆C中心在原点，以A，B为焦点，过A作直线交C于M，N两点，线段MN的中点到y轴的距离为$\frac{4}{5}$，且直线MN与E点的轨迹相切，求椭圆C方程．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    2．已知直线l1：ax-y-1=0：，l2：（a+2）x-ay+2=0（a＞0），直线l1∥l2．
    （1）求实数a的值；
    （2）是否存在一点P，它同时满足下列三个条件：①是第一象限的点：②在直线y=x上：③到直线l1的距离是它到直线l2距离的2倍．若存在．求出点P的坐标：若不存在．说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    19．已知一块四边形园地ABCD中，∠A=45°，∠B=60°，∠C=105°，若AB=2m，BC=1m，则该四边形园地ABCD的面积等于$\frac{3}{2}$-$\frac{\sqrt{3}}{4}$m2．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    6．已知数列{an+n}是首项为2，公比为2的等比数列．
    （1）求数列{an}的通项公式；
    （2）求a1+a2+a3+…+an的和．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

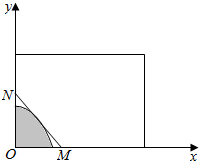    16．如图，某房地产公司要在一块矩形宽阔地面上开发物业，阴影部分是不能开发的古建筑群，且要求用在一条直线上的栏栅进行隔离，古建筑群的边界为曲线y=1-$\frac{4}{3}$x2的一部分，栏栅与矩形区域边界交于点M、N，则当能开发的面积达到最大时，OM的长为1．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    3．设α∈（π，2π），则$\sqrt{\frac{1-cos（π+α）}{2}}$等于（　　）
    A．sin$\frac{α}{2}$B．cos$\frac{α}{2}$C．-sin$\frac{α}{2}$D．-cos$\frac{α}{2}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    20．已知锐角△ABC中，S△ABC=8，AB=4，AC=5，那么BC=$\sqrt{17}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    1．定义在R上的偶函数f（x），对任意实数x都有f（x+2）=f（x），当x∈[0，1]时，f（x）=x2，若在区间[-1，3]内，函数g（x）=f（x）-kx-k有4个零点，则实数k的取值范围是（　　）
    A．$（-\frac{1}{4}，\frac{1}{4}]$B．$（0，\frac{1}{4}]$C．$（\frac{1}{4}，\frac{1}{3}]$D．$（0，\frac{1}{3}）$

    查看答案和解析>>

    同步练习册答案