
分析 (1)由题意利用两条直线平行的条件,求得a的值.
(2)由题意利用点到直线的距离公式求得m的值,从而得出结论.
解答 解:(1)由直线l1:ax-y-1=0:,l2:(a+2)x-ay+2=0(a>0),直线l1∥l2,
可得$\frac{a+2}{a}$=$\frac{-a}{-1}$≠$\frac{2}{-1}$,求得a=2,或a=-1 (舍去).
当a=2 时,直线l1:2x-y-1=0:,l2:2x-y+1=0,满足直线l1∥l2.
故a=2.
(2)设点P(m,m),m>0,由$\frac{|2m-m-1|}{\sqrt{5}}$=2•$\frac{|2m-m+1|}{\sqrt{5}}$,
可得|m-1|=2|m+1|,m2-2m+1=4(m2+2m+1),求得m=-$\frac{1}{3}$,或m=-3,
都不满足m>0,故点P不存在.
点评 本题主要考查两条直线平行的条件,点到直线的距离公式的应用,属于基础题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -2 | B. | 0 | C. | 1 | D. | 6 |
查看答案和解析>>
科目:高中数学 来源:2017届湖南衡阳八中高三上学期月考二数学(文)试卷(解析版) 题型:选择题
设函数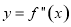 是
是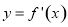 的导数.某同学经过探究发现,任意一个三次函数
的导数.某同学经过探究发现,任意一个三次函数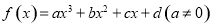 都有对称中心
都有对称中心 ,其中
,其中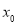 满足
满足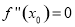 .已知函数
.已知函数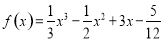 ,则
,则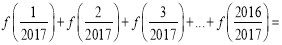 ( )
( )
A.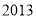 B.
B.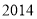 C.
C.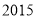 D.
D.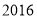
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com