
已知函数 .
.
⑴当 时,①若
时,①若 的图象与
的图象与 的图象相切于点
的图象相切于点 ,求
,求 及
及 的值;
的值;
② 在
在 上有解,求
上有解,求 的范围;
的范围;
⑵当 时,若
时,若 在
在 上恒成立,求
上恒成立,求 的取值范围.
的取值范围.
(1)①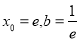 ,②
,②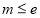 时,
时,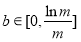 ;
;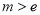 时,
时,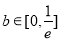 (2)
(2)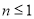 时,
时,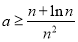 ;
;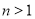 时,
时,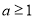 ..
..
【解析】
试题分析:(1)①本题为曲线切线问题,一般从设切点出发,利用切点在切线上.切点在曲线上,切点处的导数值为切线的斜率三个方面建立等量关系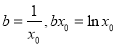 ,从而解出
,从而解出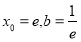 ,②方程有解问题,一般利用分离法,求函数
,②方程有解问题,一般利用分离法,求函数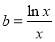 值域解决.由于定义域
值域解决.由于定义域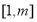 不定,需讨论极值为零的点
不定,需讨论极值为零的点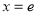 是否在定义域内,这决定了单调区间,也决定了最值.(2)不等式恒成立问题,往往转化为最值问题,这也需要分离变量. 即
是否在定义域内,这决定了单调区间,也决定了最值.(2)不等式恒成立问题,往往转化为最值问题,这也需要分离变量. 即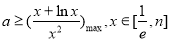 ,在求函数
,在求函数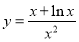 值域时,有两个难点,一是判断极值为零的点
值域时,有两个难点,一是判断极值为零的点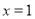 ,二是讨论极值为零的点
,二是讨论极值为零的点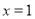 是否在
是否在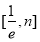 内.
内.
试题解析:⑴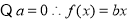
①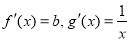
 , 3分
, 3分
②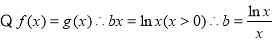 即
即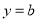 与
与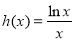 在
在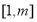 上有交点…4分
上有交点…4分
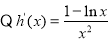 ,
,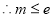 时
时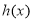 在
在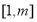 上递增,
上递增,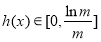 ;
;
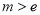 时
时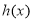 在
在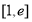 上递增,在
上递增,在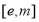 上递减且
上递减且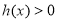 ,
,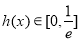 ……7分
……7分
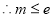 时,
时,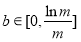 ;
;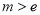 时,
时,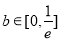 8分
8分
⑵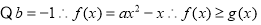 即
即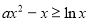 ,
,
即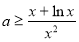 在
在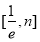 上恒成立, 9分
上恒成立, 9分
令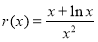 ,
,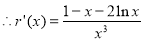
令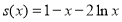 ,则
,则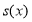 为单调减函数,且
为单调减函数,且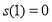 , 12分
, 12分
∴当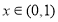 时,
时,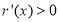 ,
,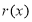 单调递增,
单调递增,
当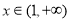 时,
时,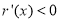 ,
,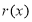 单调递减, 13分
单调递减, 13分
若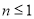 ,则
,则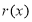 在
在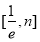 上单调递增,
上单调递增,
∴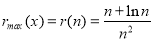 ,∴
,∴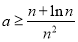 ;
;
若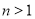 ,则
,则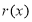 在
在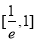 上单调递增,
上单调递增,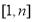 单调递减,
单调递减,
∴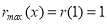 ,∴
,∴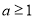 15分
15分
∴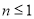 时,
时,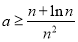 ;
;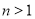 时,
时,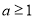 . 16分
. 16分
考点:利用导数求切线,利用导数求最值.


 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案科目:高中数学 来源:2015届江苏淮安市高二上学期期中考试数学试卷(解析版) 题型:填空题
下列四个条件中,能确定一个平面的只有 (填序号).
①空间中的三点 ②空间中两条直线 ③一条直线和一个点 ④两条平行直线
查看答案和解析>>
科目:高中数学 来源:2015届江苏扬州市高二第一学期期末调研考试数学试卷(解析版) 题型:解答题
根据我国发布的《环境空气质量指数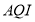 技术规定》(试行),
技术规定》(试行),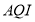 共分为六级:
共分为六级: 为优,
为优,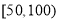 为良,
为良,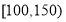 为轻度污染,
为轻度污染,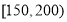 为中度污染,
为中度污染, 均为重度污染,
均为重度污染,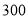 及以上为严重污染.某市2013年11月份
及以上为严重污染.某市2013年11月份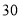 天的
天的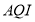 的频率分布直方图如图所示:
的频率分布直方图如图所示:

⑴该市11月份环境空气质量优或良的共有多少天?
⑵若采用分层抽样方法从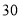 天中抽取
天中抽取 天进行市民户外晨练人数调查,则中度污染被抽到的天数共有多少天?
天进行市民户外晨练人数调查,则中度污染被抽到的天数共有多少天?
⑶空气质量指数低于 时市民适宜户外晨练,若市民王先生决定某天早晨进行户外晨练,则他当天适宜户外晨练的概率是多少?
时市民适宜户外晨练,若市民王先生决定某天早晨进行户外晨练,则他当天适宜户外晨练的概率是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com