Question

12．如图，四棱锥P-ABCD的底面是矩形，侧面PAD是正三角形，且侧面PAD⊥底面ABCD，E为侧棱PD的中点．
（1）求证：PB∥平面EAC；
（2）求证：AE⊥平面PCD；
（3）若直线AC与平面PCD所成的角为30°，求$\frac{CD}{AD}$的值．

Answer 1

分析 （1）连结BD交AC于O，连结EO，可证EO∥PB，即可证明PB∥平面EAC．
（2）要证明AE⊥平面PCD，只要证明AE?面PAD，且平面PAD⊥平面PDC即可．
（3）由（2）可得直线AC与平面PCD所成的角为∠ACE，可求$正△PAD中，AE=\frac{{\sqrt{3}}}{2}AD$，$AC=\sqrt{3}AD$，又$\sqrt{A{D^2}+C{D^2}}=\sqrt{3}AD$，解得$CD=\sqrt{2}AD$，从而求得$\frac{CD}{AD}=\sqrt{2}$．

解答 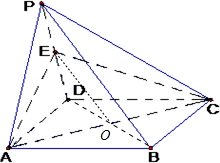解：（1）连结BD交AC于O，连结EO，
∵O、E分别为BD、PD的中点，
∴EO∥PB，E0?平面EAC，PB?平面EAC，
∴PB∥平面EAC．…．（6分）
（2）∵$\left.\begin{array}{l}矩形ABCD⇒CD⊥AD\\ 面PAD∩面ABCD=AD\\ 面ABCD⊥面PAD\end{array}\right\}\left.{\begin{array}{l}{⇒CD⊥面PAD}\\{CD?面PDC}\end{array}}\right\}⇒面PDC⊥面PAD$，CD?面ABCD，正三角形PAD中，E为PD的中点，
∴AE⊥PD，
又面PDC∩面PAD=PD，AE?面PAD，
∴AE⊥平面PCD…．（10分）
（3）由（2）AE⊥平面PCD，直线AC与平面PCD所成的角为∠ACE．
∴Rt△ACE中，∠ACE=30°，AC=2AE，又$正△PAD中，AE=\frac{{\sqrt{3}}}{2}AD$，
∴$AC=\sqrt{3}AD$，又矩形$ABCD中，AC=\sqrt{A{D^2}+C{D^2}}$，由$\sqrt{A{D^2}+C{D^2}}=\sqrt{3}AD$，
解得$CD=\sqrt{2}AD$，
∴$\frac{CD}{AD}=\sqrt{2}$…..（14分）

点评 本题主要考查了直线与平面平行的判定，直线与平面垂直的判定，考查了空间想象能力和推论论证能力，属于基本知识的考查．