
【题目】对于无穷数列![]() ,记
,记![]() ,若数列
,若数列![]() 满足:“存在
满足:“存在![]() ,使得只要
,使得只要![]() (
(![]() 且
且![]() ),必有
),必有![]() ”,则称数列
”,则称数列![]() 具有性质
具有性质![]() .
.
(Ⅰ)若数列![]() 满足
满足![]() 判断数列
判断数列![]() 是否具有性质
是否具有性质![]() ?是否具有性质
?是否具有性质![]() ?
?
(Ⅱ)求证:“![]() 是有限集”是“数列
是有限集”是“数列![]() 具有性质
具有性质![]() ”的必要不充分条件;
”的必要不充分条件;
(Ⅲ)已知![]() 是各项为正整数的数列,且
是各项为正整数的数列,且![]() 既具有性质
既具有性质![]() ,又具有性质
,又具有性质![]() ,求证:存在整数
,求证:存在整数![]() ,使得
,使得![]() 是等差数列.
是等差数列.
【答案】(Ⅰ)数列![]() 不具有性质
不具有性质![]() ;具有性质
;具有性质![]() ;(Ⅱ)见解析;(Ⅲ)见解析.
;(Ⅱ)见解析;(Ⅲ)见解析.
【解析】试题分析:(1)根据新定义直接验证即可的结论(2)对于“![]() 是有限集”是“数列
是有限集”是“数列![]() 具有性质
具有性质![]() ”的必要不充分条件,先证不充分性对于周期数列
”的必要不充分条件,先证不充分性对于周期数列![]() ,
, ![]() 是有限集,但是由于
是有限集,但是由于![]() ,
,
所以不具有性质![]() ;再证必要性因为数列
;再证必要性因为数列![]() 具有性质
具有性质![]() ,所以一定存在一组最小的
,所以一定存在一组最小的![]() 且
且![]() ,满足
,满足![]() ,即
,即![]() ,所以数列
,所以数列![]() 中必然会以某个周期进行,所以数列
中必然会以某个周期进行,所以数列![]() 中最多有
中最多有![]() 个不同的项,从而得证(3)因为数列
个不同的项,从而得证(3)因为数列![]() 具有性质
具有性质![]() ,数列
,数列![]() 具有性质
具有性质![]() ,所以存在
,所以存在![]() ,使得
,使得![]() ,
, ![]() ,其中
,其中![]() 分别是满足上述关系式的最小的正整数,然后根据其性质列出相关等式可得结论,然后逐一分析取值讨论
分别是满足上述关系式的最小的正整数,然后根据其性质列出相关等式可得结论,然后逐一分析取值讨论
试题解析:
(Ⅰ)数列![]() 不具有性质
不具有性质![]() ;具有性质
;具有性质![]() .
.
(Ⅱ)(不充分性)对于周期数列![]() ,
, ![]() 是有限集,但是由于
是有限集,但是由于![]() ,
,
所以不具有性质![]() ;
;
(必要性)因为数列![]() 具有性质
具有性质![]() ,
,
所以一定存在一组最小的![]() 且
且![]() ,满足
,满足![]() ,即
,即![]()
由性质![]() 的含义可得
的含义可得![]()
所以数列![]() 中,从第k项开始的各项呈现周期性规律:
中,从第k项开始的各项呈现周期性规律: ![]() 为一个周期中的各项,
为一个周期中的各项,
所以数列![]() 中最多有
中最多有![]() 个不同的项,
个不同的项,
所以![]() 最多有
最多有![]() 个元素,即
个元素,即![]() 是有限集.
是有限集.
(Ⅲ)因为数列![]() 具有性质
具有性质![]() ,数列
,数列![]() 具有性质
具有性质![]() ,
,
所以存在![]() ,使得
,使得![]() ,
, ![]() ,其中
,其中![]() 分别是满足上述关系式的最小的正整数,
分别是满足上述关系式的最小的正整数,
由性质![]() 的含义可得
的含义可得![]() ,
, ![]() ,
,
若![]() ,则取
,则取![]() ,可得
,可得![]() ;
;
若![]() ,则取
,则取![]() ,可得
,可得![]() .
.
记![]() ,则对于
,则对于![]() ,有
,有![]() ,
, ![]() ,显然
,显然![]() ,
,
由性质![]() 的含义可得
的含义可得![]() ,
, ![]() ,
,
所以![]()
![]()
所以![]() .
.
所以![]() ,
,
又![]() 是满足
是满足![]() ,
, ![]() 的最小的正整数,
的最小的正整数,
所以![]() ,
,
![]() ,
,
所以![]() ,
, ![]() ,
,
所以![]() ,
, ![]() ,
, ![]() ,
,
取![]() ,则
,则![]() ,
,
所以,若![]() 是偶数,则
是偶数,则![]() ;
;
若![]() 是奇数,则
是奇数,则![]() ,
,
所以![]() ,
, ![]()
所以![]() 是公差为1的等差数列.
是公差为1的等差数列.


 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
,![]() .
.
(1).当![]() 时,求
时,求![]() 的单调增区间;
的单调增区间;
(2)当![]() ,对于任意
,对于任意![]() ,都有
,都有![]() ,求实数
,求实数![]() 的取值范围;
的取值范围;
(3)若函数![]() 的图象始终在直线
的图象始终在直线![]() 的下方,求实数
的下方,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】学校为测评班级学生对任课教师的满意度,采用“100分制”打分的方式来计分.现从某班学生中随机抽取10名,以下茎叶图记录了他们对某教师的满意度分数(以十位数字为茎,个位数字为叶):
规定若满意度不低于98分,测评价该教师为“优秀”.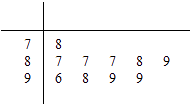
(1)求从这10人中随机选取3人,至多有1人评价该教师是“优秀”的概率;
记ξ表示抽到评价该教师为“优秀”的人数,求ξ的分布列及数学期望.
(2)以这10人的样本数据来估计整个班级的总体数据,若从该班任选3人,
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆C的极坐标方程为ρ=2cosθ,直线l的参数方程为 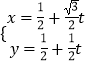 (t为参数),点A的极坐标为(
(t为参数),点A的极坐标为( ![]() ,
, ![]() ),设直线l与圆C交于点P、Q.
),设直线l与圆C交于点P、Q.
(1)写出圆C的直角坐标方程;
(2)求|AP||AQ|的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,三棱锥P﹣ABC中,PC⊥平面ABC,PC=3,∠ACB= ![]() .D,E分别为线段AB,BC上的点,且CD=DE=
.D,E分别为线段AB,BC上的点,且CD=DE= ![]() ,CE=2EB=2
,CE=2EB=2 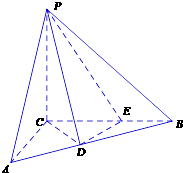
(1)证明:DE⊥平面PCD
(2)求二面角B﹣PD﹣C的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=ln(1+x),g(x)=xf′(x),x≥0,其中f′(x)是f(x)的导函数.
(1)若f(x)≥ag(x)恒成立,求实数a的取值范围;
(2)设n∈N* , 证明: ![]() +
+ ![]() +…+
+…+ ![]() <ln(n+1).
<ln(n+1).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com