练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】已知函数f（x）=（xR），g（x）=2a-1

    （1）求函数f（x）的单调区间与极值．

    （2）若f（x）≥g（x）对恒成立，求实数a的取值范围.

    【答案】(1) 函数f(x)的单调增区间为，单调减区间为.

    f（x）的极大值为6，极小值-26；(2)

    【解析】试题分析：(1)求出函数的导数，解关于导函数的不等式，即可得到函数f（x）的单调区间与极值；（2）根据函数的单调性求出端点值和极值，从而求出f（x）的最小值，得到关于a的不等式，求出a的范围即可.

    试题解析：

    （1）令，解得或，

    令，解得：.

    故函数的单调增区间为，单调减区间为.

    f（x）的极大值为f（-1）=6，极小值f（3）=-26

    （2）由（1）知在上单调递增，在上单调递减，在上单调递增，

    又，，，

    ∴，

    ∵对恒成立，

    ∴，即，∴

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】下列命题正确的个数是（ ）
    ①命题“x0∈R，x02+1＞3x0”的否定是“x∈R，x2+1≤3x”；
    ②“函数f（x）=cos2ax﹣sin2ax的最小正周期为π”是“a=1”的必要不充分条件；
    ③x2+2x≥ax在x∈[1，2]上恒成立（x2+2x）min≥（ax）max在x∈[1，2]上恒成立；
    ④“平面向量 与 的夹角是钝角”的充分必要条件是“ ＜0”．
    A.1
    B.2
    C.3
    D.4

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在直角坐标系xoy中，直线l经过点P（﹣1，0），其倾斜角为α，在以原点O为极点，x轴非负半轴为极轴的极坐标系中（取相同的长度单位），曲线C的极坐标方程为ρ2﹣6ρcosθ+1=0． （Ⅰ）若直线l与曲线C有公共点，求α的取值范围；
    （Ⅱ）设M（x，y）为曲线C上任意一点，求x+y的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】一个棱锥的三视图如图,则该棱锥的全面积为(　 )

    A. B.

    C. D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知数列的前n项和， 是等差数列，且.

    （Ⅰ）求数列的通项公式；

    （Ⅱ）令.求数列的前n项和.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，椭圆的左、右焦点为， ，右顶点为，上顶点为，若， 与轴垂直，且.

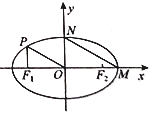
    (1)求椭圆的方程；

    (2)过点且不垂直与坐标轴的直线与椭圆交于， 两点，已知点，当时，求满足的直线的斜率的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】潮州统计局就某地居民的月收入调查了人，并根据所得数据画了样本的频率分

    布直方图（每个分组包括左端点，不包括右端点，如第一组表示收入在）。

    （1）求居民月收入在的频率；

    （2）根据频率分布直方图算出样本数据的中位数；

    （3）为了分析居民的收入与年龄、职业等方面的关系，必须按月收入再从这人中分层抽样方法抽出人作进一步分析，则月收入在的这段应抽多少人？

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数 是奇函数，若函数f（x）在区间[﹣1，a﹣2]上单调递增，则实数a的取值范围是

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设为函数两个不同零点.

    （1）若，且对任意,都有，求；

    （2）若，则关于的方程是否存在负实根?若存在,求出该负根的取值范围，若不存在，请说明理由；

    （3）若，且当时，的最大值为，求的最小值.

    查看答案和解析>>

    同步练习册答案