
分析 (1)(1)令x=y=1,根据函数f(x)(x∈R,且x>0),对于定义域内任意x、y恒有f(xy)=f(x)+f(y),我们易构造关于f(1)的方程,解方程即可求出求f(1);
(2)易将不等式f($\frac{{{x^2}+2x+a}}{x}$)>f(1)转化为a>-x2-x在x∈[1,+∞)时恒成立,根据二次函数的性质,我们即可求出实数a的取值范围.
解答 解:(1)∵定义域内任意x、y恒有f(xy)=f(x)+f(y),
令x=y=1,
∴f(1)=2f(1),
∴f(1)=0;
(2)任取0<x1<x2,则$\frac{{x}_{2}}{{x}_{1}}$>1,则题意得f($\frac{{x}_{2}}{{x}_{1}}$)>0,
又定义域内任意x、y恒有f(xy)=f(x)+f(y),
∴f(xy)-f(y)=f(x),
∴f(x2)-f(x1)=f($\frac{{x}_{2}}{{x}_{1}}$)>0,
∴f(x2)>f(x1),
∴函数f(x)在其定义域内为增函数,由(1)和f(1)=0,
当x∈[1,+∞)时,不等式f($\frac{{{x^2}+2x+a}}{x}$)>f(1)恒成立,
即$\frac{{{x^2}+2x+a}}{x}$)>1恒成立,
即x2+2x+a>x,即a>-x2-x在x∈[1,+∞)时恒成立,
∵-x2-x在x∈[1,+∞)时最大值为-2,
∴a>-2.
点评 本题考查的知识点是抽象函数及其应用,函数单调性的性质,其中(1)的关键是“凑配”思想的应用,(2)的关键是利用函数的单调性对不等式f($\frac{{{x^2}+2x+a}}{x}$)>f(1)进行变形,是一道中档题.


 名题金卷系列答案
名题金卷系列答案 优加精卷系列答案
优加精卷系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 64 | B. | 100 | C. | 36 | D. | 136 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
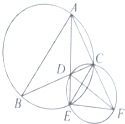 如图,在△ABC中,∠BAC的平分线交BC于点D,交△ABC的外接圆于点E,延长AC交△DCE的外接圆于点F,DF=$\sqrt{14}$.
如图,在△ABC中,∠BAC的平分线交BC于点D,交△ABC的外接圆于点E,延长AC交△DCE的外接圆于点F,DF=$\sqrt{14}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com