解答:
解:(1)当a=-1时,f(x)=x
2-x-lnx,定义域为(0,+∞),
∴f′(x)=2x-1-
=
=
,
∴当0<x<1,时f′(x)<0,当x>1时,f′(x)>0,
∴f(x)在(0,1)上单调递减,在(1,+∞)上单调递增,
∴在x=1时,f(x)有极小值,且极小值f(x)=f(1)=0;
(2)F(x)=
=
,定义域为(0,+∞),
F′(x)=
,
令h(x)=
-x2+(2-a)x+a-+lnx,则h′(x)=-2x+
++2-a,
h
″(x)=-2-
-<0,故h′(x)在区间(0,1]上单调递减,
从而对(0,1],h′(x)≥h′(1)=2-a
①当2-a≥0,即a≤2时,h′(x)≥0,∴y=h(x)在区间(0,1]上单调递增,
∴h(x)≤h(1)=0,即F′(x)≤0,
∴y=F(x)在区间(0,1]上是减函数,a≤2满足题意;
②当2-a<0,即a>2时,由h′(1)<0,h′(
)=
-+a2+2>0,
0<<1,
且y=h′(x)在区间(0,1]的图象是一条连续不断的曲线,
∴y=h′(x)在区间(0,1]有唯一零点,设为x
0,
∴h(x)在区间(0,x
0)上单调递增,在(x
0,1]上单调递减,
∴h(x
0)>h(1)=0,而h(e
-a)=-e
-2a+(2-a)e
-a+a-e
a+lne
-a<0,
且y=h(x)在区间(0,1]的图象是一条连续不断的曲线,
y=h(x)在区间(0,1)有唯一零点,设为x′,
即y=F′(x)在区间(0,1)有唯一零点,设为x′,
又F(x)在区间(0,x′)上单调递减,在(x′,1)上单调递增,
矛盾,a>2不合题意;
综上所得:a的取值范围为(-∞,2].



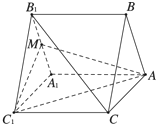 如图,三棱柱ABC-A1B1C1的底面是正三角形,AA1⊥底面ABC,M为A1B1的中点.
如图,三棱柱ABC-A1B1C1的底面是正三角形,AA1⊥底面ABC,M为A1B1的中点.