
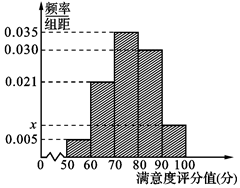
 共享单车是指由企业在校园、公交站点、商业区、公共服务区等场所提供的自行车单车共享服务,由于其依托“互联网+”,符合“低碳出行”的理念,已越来越多地引起了人们的关注.某部门为了对该城市共享单车加强监管,随机选取了100人就该城市共享单车的推行情况进行问卷调查,并将问卷中的这100人根据其满意度评分值(百分制)按照 分成5组,制成如图所示频率分直方图.
共享单车是指由企业在校园、公交站点、商业区、公共服务区等场所提供的自行车单车共享服务,由于其依托“互联网+”,符合“低碳出行”的理念,已越来越多地引起了人们的关注.某部门为了对该城市共享单车加强监管,随机选取了100人就该城市共享单车的推行情况进行问卷调查,并将问卷中的这100人根据其满意度评分值(百分制)按照 分成5组,制成如图所示频率分直方图.分析 (1)频率和为1列出方程求得x的值;
(2)计算满意度评分值在内的人数,写出X的值可能取值,
计算对应的概率值,写出分布列,计算数学期望值.
解答 解析:(1)由(0.005+0.021+0.035+0.030+x)×10=1,
解得x=0.009;
(2)满意度评分值在内有100×0.009×10=9人,
其中男生6人,女生3人;
则X的值可以为0,1,2,3;
计算$P({X=0})=\frac{C_6^4C_3^0}{C_9^4}=\frac{15}{126}$,
$P({X=1})=\frac{C_6^3C_3^1}{C_9^4}=\frac{60}{126}$,
$P({X=2})=\frac{C_6^2C_3^2}{C_9^4}=\frac{45}{126}$,
$P({X=3})=\frac{C_6^1C_3^3}{C_9^4}=\frac{6}{126}$;
则X分布列如下:
| X | 0 | 1 | 2 | 3 |
| P | $\frac{15}{126}$ | $\frac{60}{126}$ | $\frac{45}{126}$ | $\frac{6}{126}$ |
点评 本题考查了频率分布直方图与离散型随机变量的分布列与数学期望的计算问题,是中档题.


科目:高中数学 来源: 题型:填空题
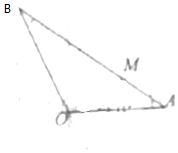 如图,在△AOB中,∠AOB=$\frac{3π}{4}$,OA=6,M为边AB上一点,M到边OA,OB的距离分别为2,2$\sqrt{2}$,则AB的长为6$\sqrt{5}$.
如图,在△AOB中,∠AOB=$\frac{3π}{4}$,OA=6,M为边AB上一点,M到边OA,OB的距离分别为2,2$\sqrt{2}$,则AB的长为6$\sqrt{5}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 等腰直角三角形 | B. | 直角三角形 | C. | 等腰三角形 | D. | 等边三角形 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 外切 | B. | 相离 | C. | 相交 | D. | 内切 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | $\frac{1}{2}$ | C. | $\frac{3}{4}$ | D. | $\frac{5}{8}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com