
分析 (1)由三角形的面积公式可得ab=4,结合余弦定理可得a+b=4,联立可解.
(2)已知条件结合三角函数公式化简可得sinBcosA=2sinAcosA,分别可得A=$\frac{π}{2}$或B=$\frac{π}{2}$,即可证明
解答 解:(1)由余弦定理及已知条件得,a2+b2-ab=4,
又因为△ABC的面积等于$\sqrt{3}$,所以$\frac{1}{2}absinC=\sqrt{3}$,得ab=4.
联立方程组$\left\{\begin{array}{l}{a^2}+{b^2}-ab=4\\ ab=4\end{array}\right.$,
解得a=2,b=2.
(2)由题意得sin(B+A)+sin(B-A)=4sinAcosA,
即sinBcosA=2sinAcosA,
当cosA=0时,$A=\frac{π}{2}$,△ABC是直角三角形;
当cosA≠0时,得sinB=2sinA=2sin(B+C)=2sinBcosC+2cosBsinC,
$C=\frac{π}{3}$代入上式得$sinB=sinB+\sqrt{3}cosB$,
故$cosB=0,B=\frac{π}{2}$,
故△ABC是直角三角形
点评 本题考查三角形的面积公式以及三角形的余弦定理,三角形形状的判断,涉及三角函数公式的应用,属中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
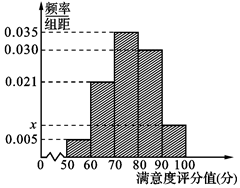 共享单车是指由企业在校园、公交站点、商业区、公共服务区等场所提供的自行车单车共享服务,由于其依托“互联网+”,符合“低碳出行”的理念,已越来越多地引起了人们的关注.某部门为了对该城市共享单车加强监管,随机选取了100人就该城市共享单车的推行情况进行问卷调查,并将问卷中的这100人根据其满意度评分值(百分制)按照 分成5组,制成如图所示频率分直方图.
共享单车是指由企业在校园、公交站点、商业区、公共服务区等场所提供的自行车单车共享服务,由于其依托“互联网+”,符合“低碳出行”的理念,已越来越多地引起了人们的关注.某部门为了对该城市共享单车加强监管,随机选取了100人就该城市共享单车的推行情况进行问卷调查,并将问卷中的这100人根据其满意度评分值(百分制)按照 分成5组,制成如图所示频率分直方图.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 9 | B. | 4 | C. | $\frac{1}{2}$ | D. | $\frac{1}{4}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com