
分析 (1)本题证明结论中结构较复杂,而其否定结构简单,故可用反证法证明其否定不成立,以此来证明结论成立.
(2)充分性:a=1时,f′(x)=$\frac{x-1}{{x}^{2}}$(x>0).利用导数研究函数的单调性极值最值可得:x=1时,函数f(x)取得极小值也是最小值.即可证明.
必要性:f(x)=0在(0,+∞)上有唯一解,且a>0,由导数的性质可得:在x=a处有极小值也是最小值f(a),f(a)=lna-a+1再利用导数研究其单调性极值与最值即可证明.
解答 证明:(1)(反证法):假设$\frac{1+x}{y}$与$\frac{1+y}{x}$均不小于2,即$\frac{1+x}{y}$≥2,$\frac{1+y}{x}$≥2,
∴1+x≥2y,1+y≥2x.将两式相加得:x+y≤2,与已知x+y>2矛盾,
故$\frac{1+x}{y}$与$\frac{1+y}{x}$中至少有一个小于2.
(2)充分性:f′(x)=$\frac{1}{x}$-a•$\frac{1}{{x}^{2}}$=$\frac{x-a}{{x}^{2}}$(x>0),
a=1时,f′(x)=$\frac{x-1}{{x}^{2}}$(x>0).
在(0,1)上单调递减,在(1,+∞)上单调递增,
∴x=1时,函数f(x)取得极小值也是最小值.
即fmin(x)=f(1)=0.
∴a=1时,函数f(x)的图象在(0,+∞)上有唯一的一个零点x=1.
必要性:f(x)=0在(0,+∞)上有唯一解,且a>0,
当a>0时,单调递增区间为(a,+∞),单调递减区间为(0,a).
在x=a处有极小值也是最小值f(a),f(a)=lna-a+1.
令g(a)=lna-a+1,g′(a)=$\frac{1}{a}$-1=$\frac{1-a}{a}$.
当0<a<1时,g′(a)>0,在(0,1)上单调递增;
当a>1时,g′(a)<0,在(1,+∞)上单调递减.
∴gmax(a)=g(1)=0,g(a)=0只有唯一解a=1.
f(x)=0在(0,+∞)上有唯一解时必有a=1.
综上:在a>0时,f(x)=0在(0,+∞)上有唯一解的充要条件是a=1.
点评 本题考查了利用导数研究函数的单调性极值与最值、两次求导的方法、等价转化方法、不等式的解法、充要条件,考查了分析问题与解决问题的能力、推理能力与计算能力,反证法证明命题,属于难题.


科目:高中数学 来源: 题型:选择题
| A. | 等腰直角三角形 | B. | 直角三角形 | C. | 等腰三角形 | D. | 等边三角形 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
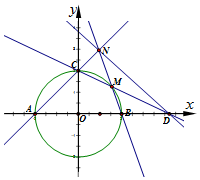 如图,圆O:x2+y2=4与坐标轴交于点A,B,C.设点M是圆上任意一点(不在坐标轴上),直线CM交x轴于点D,直线BM交直线AC于点N.
如图,圆O:x2+y2=4与坐标轴交于点A,B,C.设点M是圆上任意一点(不在坐标轴上),直线CM交x轴于点D,直线BM交直线AC于点N.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | $\frac{1}{2}$ | C. | $\frac{3}{4}$ | D. | $\frac{5}{8}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com