
分析 (Ⅰ)若a=1,b=c,则|f(1)|=|1+b+b|≤1,f(x)的对称轴$x=-\frac{b}{2}∈[0,\frac{1}{2}]$,进而求得实数b的取值范围;
(Ⅱ)由当|x|≤1时,|f(x)|≤1恒成立,可知|f(-1)|≤1,|f(0)|≤1,|f(1)|≤1,利用放缩法,可得当x=0时,g(x)=|-x2+2|取到最大值2.
解答 解:(Ⅰ)由a=1且b=c,得$f(x)={x^2}+bx+b={(x+\frac{b}{2})^2}+b-\frac{b^2}{4}$,…(1分)
当x=1时,|f(1)|=|1+b+b|≤1,得-1≤b≤0. …(3分)
故f(x)的对称轴$x=-\frac{b}{2}∈[0,\frac{1}{2}]$,
所以当|x|≤1时,$\left\{\begin{array}{l}f{(x)_{min}}=f(-\frac{b}{2})=b-\frac{b^2}{4}≥-1\\ f{(x)_{max}}=f(-1)=1≤1.\end{array}\right.$,…(5分)
解得 $2-2\sqrt{2}≤b≤2+2\sqrt{2}$…(6分)
综上,实数b的取值范围为$[2-2\sqrt{2},0]$. …(7分)
(Ⅱ)由当|x|≤1时,|f(x)|≤1恒成立,可知|f(-1)|≤1,|f(0)|≤1,|f(1)|≤1,…(8分)
且由 f(-1)=a-b+c,f(0)=c,f(1)=a+b+c,
解得$a=\frac{f(-1)+f(1)-2f(0)}{2}$,$b=\frac{f(1)-f(-1)}{2}$,c=f(0).…(10分)
故$g(x)=|{f(0){x^2}-\frac{f(1)-f(-1)}{2}x+\frac{f(-1)+f(1)-2f(0)}{2}}|$
$\begin{array}{l}≤|{f(0)({x^2}-1)}|+|{\frac{f(-1)-f(1)}{2}x+\frac{f(-1)+f(1)}{2}}|\\≤|{f(0)}||{{x^2}-1}|+max\{|{f(-1)}|,|{f(1)}|\}\end{array}$
≤1+1=2…(14分)
且当a=2,b=0,c=-1时,若|x|≤1,则|f(x)|=|2x2-1|≤1恒成立,
且当x=0时,g(x)=|-x2+2|取到最大值2.
所以,g(x)的最大值为2. …(15分)
点评 本题考查的知识点是二次函数的图象和性质,分段函数的应用,恒成立问题,最值问题,综合性可,难度较大.


 考前必练系列答案
考前必练系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | x0∈(-4,-3) | B. | x0∈(-3,-2) | C. | x0∈(-2,-1) | D. | x0∈(-1,0) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
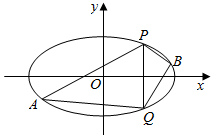 已知椭圆C的中心在原点,焦点在x轴上,离心率为$\frac{\sqrt{3}}{2}$,它的一个顶点恰好是抛物线x2=4$\sqrt{2}$y的焦点.
已知椭圆C的中心在原点,焦点在x轴上,离心率为$\frac{\sqrt{3}}{2}$,它的一个顶点恰好是抛物线x2=4$\sqrt{2}$y的焦点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com