
分析 若狼的数量不少于羊的数量,狼会吃羊,那么羊的数量要一直多于狼的数量,先把2只狼带到对岸,然后人自己返回,再一只羊带到对岸,然后把两只狼带回;再把两只羊带到对岸,然后人自己返回,再把3只狼份两次运到对岸即可.
解答 解:人和动物同船不用考虑动物的争斗,但需考虑承载的数量,还应考虑到两岸的动物都得保证狼的数量要小于羚羊的数量,故在算法的构造中应尽可能保证船里面有狼,这样才能使得两岸的羚羊数量占到优势,具体算法如下:
第一步,人带两只狼过河,自己返回.
第二步,人带一只羚羊过河,带2只狼返回.
第三步,人带两只羚羊过河,自己返回.
第四步,人带带2只狼过河,自己返回.
第五步,人带1只狼过河.
点评 本题主要考查了设计程序算法解决实际问题,解决本题抓住羊的数量要一直多于羊的数量这一特点,进行求解即可,属于基础题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | 8 | C. | $3\sqrt{2}$ | D. | 10 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
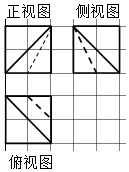 如图所示,网格线上小正方形边长为1,用两个平面去截正方体,所得的几何体的三视图为粗线部分,则此几何体的体积为( )
如图所示,网格线上小正方形边长为1,用两个平面去截正方体,所得的几何体的三视图为粗线部分,则此几何体的体积为( )| A. | $\frac{20}{3}$ | B. | $\frac{19}{3}$ | C. | 6 | D. | $\frac{17}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{8}$ | B. | $\frac{3}{4}$ | C. | $-\frac{1}{8}$ | D. | $-\frac{3}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 6 | B. | 3 | C. | $\frac{8}{3}$ | D. | $\frac{4}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com