
分析 (1)由题意可得b=$\sqrt{3}$,运用正三角形的性质可得c=btan30°=1,求得a=2,进而得到椭圆方程;
(2)设直线PB的方程为y=k(x-4)联立$\left\{\begin{array}{l}{y=k(x-4)}\\{3{x}^{2}+4{y}^{2}=12}\end{array}\right.$,设点B(x1,y1),E(x2,y2),通过韦达定理求出直线方程,即可求出定点坐标.
解答 解:(1)椭圆C过点$M({0,\sqrt{3}})$,可得b=$\sqrt{3}$,
△MF1F2为正三角形,可得c=btan30°=$\sqrt{3}$×$\frac{\sqrt{3}}{3}$=1,
a=$\sqrt{{b}^{2}+{c}^{2}}$=2,即有椭圆C的方程为$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{3}$=1;
(2)由题意知直线PB的斜率存在,设直线PB的方程为y=k(x-4),
联立$\left\{\begin{array}{l}{y=k(x-4)}\\{3{x}^{2}+4{y}^{2}=12}\end{array}\right.$,得(4k2+3)x2-32k2x+64k2-12=0①
设点B(x1,y1),E(x2,y2),则A(x1,-y1),
直线AE的方程为y-y2=$\frac{{y}_{2}+{y}_{1}}{{x}_{2}-{x}_{1}}$(x-x2),
令y=0,得x=x2-$\frac{{y}_{2}({x}_{2}-{x}_{1})}{{y}_{2}+{y}_{1}}$,
再将y1=k(x1-4),y2=k(x2-4)代入
整理得x=$\frac{2{x}_{1}{x}_{2}-4({x}_{1}+{x}_{2})}{{x}_{1}+{x}_{2}-8}$②
由①得x1+x2=$\frac{32{k}^{2}}{3+4{k}^{2}}$,x1x2=$\frac{64{k}^{2}-12}{3+4{k}^{2}}$,
代入②整理得x=1,
所以直线AE与x轴相交于定点(1,0).
点评 本题考查直线方程与椭圆方程的综合应用,椭圆的标准方程的求法,考查分析问题解决问题的能力.


科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 1 | C. | 2 | D. | 0或 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
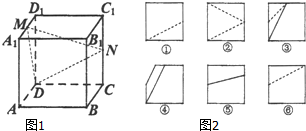
| A. | ①④⑤ | B. | ②③⑥ | C. | ①③⑤ | D. | ②④⑥ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (1,0) | B. | (-1,-4) | C. | (1,0)或(-1,-4) | D. | (1,4) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | x0∈(-4,-3) | B. | x0∈(-3,-2) | C. | x0∈(-2,-1) | D. | x0∈(-1,0) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com