
【题目】选修4—4:坐标系与参数方程
在平面直角坐标系中,圆C的方程为 (θ为参数).以坐标原点O为极点,
(θ为参数).以坐标原点O为极点, ![]() 轴的正半轴为极轴,建立极坐标系,两种坐标系中取相同的单位长度,直线
轴的正半轴为极轴,建立极坐标系,两种坐标系中取相同的单位长度,直线![]() 的极坐标方程
的极坐标方程![]() .
.
(Ⅰ)当![]() 时,判断直线
时,判断直线![]() 与
与![]() 的关系;
的关系;
(Ⅱ)当![]() 上有且只有一点到直线
上有且只有一点到直线![]() 的距离等于
的距离等于![]() 时,求
时,求![]() 上到直线
上到直线![]() 距离为
距离为![]() 的点的坐标.
的点的坐标.
【答案】(1)见解析;(2)(2,0)和(0,2).
【解析】试题分析:(I)将曲线方程化成直角坐标方程,计算圆心到直线的距离与圆的半径比较大小得出结论;
(II)由题意可知直线与圆相离,且圆心到直线l的距离为2![]() ,故到直线l的距离等于2
,故到直线l的距离等于2![]() 的点在过圆心且与直线l平行的直线上,求出此直线的参数方程代入圆的方程求出该点对应的参数,得出该点的坐标.
的点在过圆心且与直线l平行的直线上,求出此直线的参数方程代入圆的方程求出该点对应的参数,得出该点的坐标.
试题解析:
(Ⅰ)圆C的普通方程为:(x-1)2+(y-1) 2=2,
直线l的直角坐标方程为:x+y-3=0,
圆心(1,1)到直线l的距离为![]()
所以直线l与C相交.
(Ⅱ) 直线l的普通方程为x+y﹣m=0.
∵C上有且只有一点到直线l的距离等于![]() ,
,
∴直线l与圆C相离,且圆心到直线的距离为![]() .
.
∴圆C上到直线l的距离等于2![]() 的点在过圆心C(1,1)且与直线l平行的直线上.
的点在过圆心C(1,1)且与直线l平行的直线上.
∴过圆心C(1,1)且与直线l平行的直线的参数方程为: 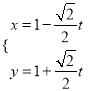 (t为参数).
(t为参数).
将: 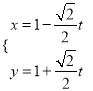 (t为参数)代入圆C的普通方程得t2=2,
(t为参数)代入圆C的普通方程得t2=2,
∴t1=![]() ,t2=﹣
,t2=﹣![]() .
.
当t=![]() 时,
时, ![]() ,当t=﹣
,当t=﹣![]() 时,
时, ![]() .
.
∴C上到直线l距离为2![]() 的点的坐标为(0,2),(2,0).
的点的坐标为(0,2),(2,0).


科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() ,且函数g(x)=loga(x2+x+2)(a>0,且a≠1)在[﹣
,且函数g(x)=loga(x2+x+2)(a>0,且a≠1)在[﹣ ![]() ,1]上的最大值为2,若对任意x1∈[﹣1,2],存在x2∈[0,3],使得f(x1)≥g(x2),则实数m的取值范围是( )
,1]上的最大值为2,若对任意x1∈[﹣1,2],存在x2∈[0,3],使得f(x1)≥g(x2),则实数m的取值范围是( )
A.(﹣∞,﹣ ![]() ]
]
B.(﹣∞, ![]() ]
]
C.[ ![]() ,+∞)
,+∞)
D.[﹣ ![]() ,+∞]
,+∞]
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,四棱锥![]() ,侧面
,侧面![]() 是边长为2的正三角形,且平面
是边长为2的正三角形,且平面![]() 平面
平面![]() ,底面
,底面![]() 是菱形,且
是菱形,且![]() ,
, ![]() 为棱
为棱![]() 上的动点,且
上的动点,且![]() .
.

(1)求证: ![]() ;
;
(2)试确定![]() 的值,使得二面角
的值,使得二面角![]() 的余弦值为
的余弦值为![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,棱柱ABCD-A1B1C1D1中,底面ABCD是平行四边形,侧棱AA1⊥底面ABCD,AB=1,AC=![]() ,BC=BB1=2.
,BC=BB1=2.

(Ⅰ)求证:AC⊥平面ABB1A1;
(Ⅱ)求点D到平面ABC1的距离d.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P﹣ABCD中,底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC=2,E是PC的中点. 
(1)求证:PA∥平面EDB;
(2)求锐二面角C﹣PB﹣D的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数y=f(x)满足f(﹣x)+f(x)=0且f(x+1)=f(x﹣1),若x∈(0,1)时,f(x)=log2 ![]() ,则y=f(x)在(1,2)内是( )
,则y=f(x)在(1,2)内是( )
A.单调增函数,且f(x)<0
B.单调减函数,且f(x)<0
C.单调增函数,且f(x)>0
D.单调增函数,且f(x)>0
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】绿色出行越来越受到社会的关注,越来越多的消费者对新能源汽车感兴趣![]() 但是消费者比较关心的问题是汽车的续驶里程
但是消费者比较关心的问题是汽车的续驶里程![]() 某研究小组从汽车市场上随机抽取20辆纯电动汽车调查其续驶里程
某研究小组从汽车市场上随机抽取20辆纯电动汽车调查其续驶里程![]() 单次充电后能行驶的最大里程
单次充电后能行驶的最大里程![]() ,被调查汽车的续驶里程全部介于50公里和300公里之间,将统计结果分成5组:
,被调查汽车的续驶里程全部介于50公里和300公里之间,将统计结果分成5组: ![]() ,绘制成如图所示的频率分布直方图.
,绘制成如图所示的频率分布直方图.
![]() 求直方图中m的值;
求直方图中m的值;
![]() 求本次调查中续驶里程在
求本次调查中续驶里程在![]() 的车辆数;
的车辆数;
![]() 若从续驶里程在
若从续驶里程在![]() 的车辆中随机抽取2辆车,求其中恰有一辆车续驶里程在
的车辆中随机抽取2辆车,求其中恰有一辆车续驶里程在![]() 的概率.
的概率.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com