
分析 (1)由题意求出$|O{P_1}|=2\sqrt{10}$,$|O{P_1}^/|=\frac{{\sqrt{10}}}{2}$,由此能求出${P_1}^/$的坐标.
(2)过点O作OQ1⊥直线y=-2x+10,垂足为Q1,设Q1的“10-相好点”为${Q_1}^/$,则$|O{Q_1}||O{Q_1}^/|=10$,由此能证明点${P_1}^/,{P_2}^/,…{P_{2017}}^/$共圆,联立$\left\{\begin{array}{l}y=-2x+10\\ y=\frac{1}{2}x\end{array}\right.$,得Q1(4,2),从而求出${Q_1}^/(2,1)$,进而求出圆C的方程.
(3)推导出$(\frac{4}{3},1)$恒在圆的内部,从而得到圆C与直线(3+3λ)x-(4+λ)y-3λ=0(λ∈R)的位置关系是相交.
解答 解:(1)由题意:$|O{P_1}|=2\sqrt{10}$,由$|O{P_1}||O{P_1}^/|=10$
则$|O{P_1}^/|=\frac{{\sqrt{10}}}{2}$
又点${P_1}^/$在直线y=3x上,且在射线OP1上,设点${P_1}^/(x,3x)$
所以$\sqrt{{x^2}+9{x^2}}=\frac{{\sqrt{10}}}{2}$,
故${P_1}^/$的坐标为${P_1}^/(\frac{1}{2},\frac{3}{2})$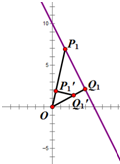
证明:(2)过点O作OQ1⊥直线y=-2x+10,垂足为Q1,设Q1的“10-相好点”为${Q_1}^/$
则$|O{Q_1}||O{Q_1}^/|=10$又∵$|O{P_1}||O{P_1}^/|=10$∴$|O{P_1}||O{P_1}^/|=|O{Q_1}||O{Q_1}^/|$即:$\frac{{|O{P_1}|}}{{|O{Q_1}|}}=\frac{{|O{Q_1}^/|}}{{|O{P_1}^/|}}$
又$∠{P_1}O{Q_1}=∠{Q_1}^/O{P_1}^/$∴$△O{P_1}{Q_1}相似△O{Q_1}^/{P_1}^/$∴$∠O{P_1}^/{Q_1}^/=∠O{Q_1}{P_1}={90^0}$∴${P_1}^/$在以$O{Q_1}^/$为直径的圆上,
同理可证:${P_2}^/,{P_3}^/,…{P_{2017}}^/$都在以$O{Q_1}^/$为直径的圆上
所以点${P_1}^/,{P_2}^/,…{P_{2017}}^/$共圆
由题意$\left\{\begin{array}{l}y=-2x+10\\ y=\frac{1}{2}x\end{array}\right.$联立求解,得Q1(4,2)
由于$|O{Q_1}||O{Q_1}^/|=10$且${Q_1}^/$在射线OQ1上
所以${Q_1}^/(2,1)$
则圆C的方程为:${(x-1)^2}+{(y-\frac{1}{2})^2}=\frac{5}{4}$
解:(3)∵直线(3+3λ)x-(4+λ)y-3λ=0(λ∈R)恒过$(\frac{4}{3},1)$
而$(\frac{4}{3},1)$恒在圆的内部.
故圆C与直线(3+3λ)x-(4+λ)y-3λ=0(λ∈R)的位置关系是相交.
点评 本题考查点的坐标的求法,考查点共圆的证明,考查圆的方程的求法,考查直线与圆的位置关系的判断,是中档题,解题时要认真审题,注意圆的性质的合理运用.


 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案科目:高中数学 来源: 题型:选择题
| A. | 3π | B. | 4π | C. | 5π | D. | 8π |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com