
分析 (1)设f(x)=ax+b(a≠0),由f(f(x))=4x-1,得a(ax+b)+b=a2x+ab+b=4x-1,然后利用系数相等列式求得a,b的值得答案;
(2)由已知可得f(0)=0,再结合函数的奇偶性及x>0时,f(x)=2x-1求得x<0时的解析式得答案.
解答 解:(1)设f(x)=ax+b(a≠0),
由f(f(x))=4x-1,得a(ax+b)+b=a2x+ab+b=4x-1,
∴$\left\{\begin{array}{l}{{a}^{2}=4}\\{ab+b=-1}\end{array}\right.$,解得$\left\{\begin{array}{l}{a=2}\\{b=-\frac{1}{3}}\end{array}\right.$或$\left\{\begin{array}{l}{a=-2}\\{b=1}\end{array}\right.$.
∴f(x)=2x$-\frac{1}{3}$或f(x)=-2x+1;
(2)由函数f(x)(x∈R)是奇函数,得f(0)=0;
又当x>0时,f(x)=2x-1,
设x<0,则-x>0,∴f(x)=-f(-x)=-(-2x-1)=2x+1.
∴$f(x)=\left\{\begin{array}{l}{2x-1,x>0}\\{0,x=0}\\{2x+1,x<0}\end{array}\right.$.
点评 本题考查函数解析式的求解及常用方法,考查了利用待定系数法求函数解析式,是中档题.


科目:高中数学 来源: 题型:选择题
| A. | (-$\frac{5π}{8}$,-$\frac{π}{8}$) | B. | (-$\frac{3π}{8}$,-$\frac{π}{8}$) | C. | (-$\frac{π}{8}$,$\frac{π}{8}$) | D. | (-$\frac{π}{8}$,$\frac{3π}{8}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 在圆内接四边形ABCD中,AC与BD交于点E,过点A作圆的切线交CB的延长线于点F,若AB=AD,AD∥FC,AF=18,BC=15,求AE的长.
在圆内接四边形ABCD中,AC与BD交于点E,过点A作圆的切线交CB的延长线于点F,若AB=AD,AD∥FC,AF=18,BC=15,求AE的长.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
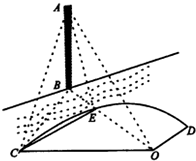 如图,河的一侧是以O为圆形,半径为80$\sqrt{3}$米的扇形区域OCD,河的另一侧有一建筑物AB垂直于水平面,假设扇形OCD与点B处于同一水平面,记OB与$\widehat{CD}$的交点为E,若在点C,点O和点E处看到点A的仰角分别为45°,30°和60°,则∠CBO的余弦值为$\frac{4\sqrt{3}}{9}$.
如图,河的一侧是以O为圆形,半径为80$\sqrt{3}$米的扇形区域OCD,河的另一侧有一建筑物AB垂直于水平面,假设扇形OCD与点B处于同一水平面,记OB与$\widehat{CD}$的交点为E,若在点C,点O和点E处看到点A的仰角分别为45°,30°和60°,则∠CBO的余弦值为$\frac{4\sqrt{3}}{9}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com