
【题目】设 ![]() 是等差数列,
是等差数列, ![]() 是各项都为正数的等比数列,且
是各项都为正数的等比数列,且 ![]() ,
, ![]() ,
, ![]()
(1)求数列 ![]() ,
, ![]() 的通项公式;
的通项公式;
(2)设数列 ![]() 的前
的前 ![]() 项和为
项和为 ![]() 试比较
试比较 ![]() 与6的大小.
与6的大小.
【答案】
(1)解:设 ![]() 的公差为
的公差为 ![]() ,
, ![]() 的公比为
的公比为 ![]() .
.
则依题意有 ![]() 且
且 ![]() ,
,
解得 ![]() ,
,
所以 ![]() ,
, ![]() .
.
(2)解: ![]() ,
,
![]() ,①
,①
![]() ,②
,②
②-①得: ![]()
![]()
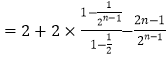
![]() .
.
【解析】(1)由题意结合等差数列和等比数列的定义求出公差和公比进而得到两个数列的通项公式。(2)根据题意整理出通项公式求出前n项和的公式,再利用等式两边乘以公比后两式相减即可求出前n项和的公式,整理该式即得到一个等比数列,根据等比数列求和公式即可求出结果。
【考点精析】解答此题的关键在于理解等差数列的前n项和公式的相关知识,掌握前n项和公式:![]() ,以及对等比数列的定义的理解,了解如果一个数列从第2项起,每一项与它的前一项的比等于同一个常数,那么这个数列就叫做等比数列.
,以及对等比数列的定义的理解,了解如果一个数列从第2项起,每一项与它的前一项的比等于同一个常数,那么这个数列就叫做等比数列.


科目:高中数学 来源: 题型:
【题目】设定点F1(0,﹣3)、F2(0,3),动点P满足条件|PF1|+|PF2|=a+ ![]() (a>0),则点P的轨迹是( )
(a>0),则点P的轨迹是( )
A.椭圆
B.线段
C.不存在
D.椭圆或线段
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如果 ![]() ,
, ![]() 是平面
是平面 ![]() 内所有向量的一组基底,那么( )
内所有向量的一组基底,那么( )
A.若实数 ![]() ,
, ![]() ,使
,使 ![]() ,则
,则 ![]()
B.空间任一向量 ![]() 可以表示为
可以表示为 ![]() ,这里
,这里 ![]() ,
, ![]() 是实数
是实数
C.![]() ,
, ![]() 不一定在平面
不一定在平面 ![]() 内
内
D.对平面 ![]() 内任一向量
内任一向量 ![]() ,使
,使 ![]() 的实数
的实数 ![]() ,
, ![]() 有无数对
有无数对
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图是函数y=f(x)的导函数y=f′(x)的图象,给出下列命题: ①﹣3是函数y=f(x)的极值点;
②﹣1是函数y=f(x)的最小值点;
③y=f(x)在x=0处切线的斜率小于零;
④y=f(x)在区间(﹣3,1)上单调递增.
则正确命题的序号是 . 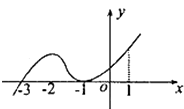
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义:在数列 ![]() 中,若
中,若 ![]()
![]() 为常数)则称
为常数)则称 ![]() 为“等方差数列”,下列是对“等方差数列”的有关判断( )
为“等方差数列”,下列是对“等方差数列”的有关判断( )
①若 ![]() 是“等方差数列”,在数列
是“等方差数列”,在数列 ![]() 是等差数列;
是等差数列;
② ![]() 是“等方差数列”;
是“等方差数列”;
③若 ![]() 是“等方差数列”,则数列
是“等方差数列”,则数列 ![]() 为常)也是“等方差数列”;
为常)也是“等方差数列”;
④若 ![]() 既是“等方差数列”又是等差数列,则该数列是常数数列.
既是“等方差数列”又是等差数列,则该数列是常数数列.
其中正确命题的个数为( )
A.1
B.2
C.3
D.4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知 m>1 且关于 x 的不等式![]() 的解集为 [0,4] .
的解集为 [0,4] .
①求 m 的值;
②若 a , b 均为正实数,且满足 a+b=m ,求 a2+b2 的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com