练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】说明：请同学们在（A）（B）两个小题中任选一题作答.

    （A）小明计划搭乘公交车回家，经网上公交实时平台查询，得到838路与611路公交车预计到达公交站的时间均为8：30，已知公交车实际到达时间与网络报时误差不超过10分钟.

    （1）若小明赶往公交站搭乘 611 路，预计小明到达站时间在8:20到8:35，求小明比车早到的概率；

    （2）求两辆车到达站时间相差不超过5分钟的概率.

    （B）小明计划搭乘公交车回家，经网上公交实时平台查询，得到838路与611路公交车预计到达公交站的之间均为8:30.已知公交车实际到达时间与网络报时误差不超过10分钟

    （1）求两辆车到达站时间相差不超过5分钟的概率

    （2）求838路与611路公交车实际到站时间与网络报时的误差之和不超过10分钟的概率。

    【答案】（A）（1） （2）（B）（1）（2）

    【解析】

    （A）（1）设公交车611路到达时间为，小明到达时间为，小明比车早到，则，由几何概型得到概率即可；（2）设611路公交车的到达时间为，838路公交车的到达时间为，两辆车相差时间不超过5分钟，则，由几何概型得到概率即可；

    （B）（1）设838路到达公交站的时刻为8点分钟，611路到达公交站的时刻为8点分钟，则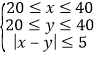，结合图形可得到两辆车到达站时间相差不超过5分钟的概率即可得解；（2）设838路公交车实际到站时刻为8点分钟，611路公交车实际到站时刻为8点分钟，则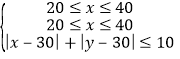，结合图形可知，838路与611路公交车实际到站时间与网络报时的误差之和不超过10分钟的概率即可得解.

    （A）（1）设公交车611路到达时间为，小明到达时间为，小明比车早到，则，由几何概型得到概率为

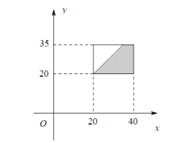
    （2）设611路公交车的到达时间为，838路公交车的到达时间为，两辆车相差时间不超过5分钟，则，.

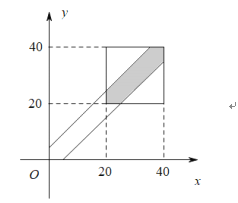
    （B）（1）设838路到达公交站的时刻为8点分钟，611路到达公交站的时刻为8点分钟，则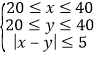

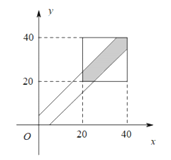
    由图可知，两辆车到达站时间相差不超过5分钟的概率

    （2）设838路公交车实际到站时刻为8点分钟，611路公交车实际到站时刻为8点分钟，则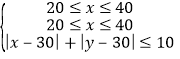

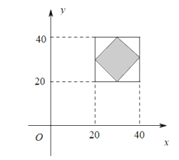
    由图可知，838路与611路公交车实际到站时间与网络报时的误差之和不超过10分钟的概率

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】对于函数，若在其定义域内存在实数，使得成立，则称有“※点”。

    （1）判断函数在上是否有“※点”。并说明理由；

    （2）若函数在上有“※点”，求正实数a的取值范围。

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数f（x）=sin（3x+ ）．
    （1）求f（x）的单调递增区间；
    （2）若α是第二象限角，f（ ）= cos（α+ ）cos2α，求cosα﹣sinα的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知P1（a1 ， b1）与P2（a2 ， b2）是直线y=kx+1（k为常数）上两个不同的点，则关于x和y的方程组 的解的情况是（ ）
    A.无论k，P1 ， P2如何，总是无解
    B.无论k，P1 ， P2如何，总有唯一解
    C.存在k，P1 ， P2 ， 使之恰有两解
    D.存在k，P1 ， P2 ， 使之有无穷多解

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】对二项式（1-x）10,

    （1）展开式的中间项是第几项？写出这一项；

    （2）求展开式中各二项式系数之和；

    （3）写出展开式中系数最大的项.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】中国南北朝时期的著作《孙子算经》中，对同余除法有较深的研究．设

    为整数，若和被除得的余数相同，则称和对模同余，记为．若，，则的值可以是

    A. 2015 B. 2016 C. 2017 D. 2018

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】(2015·湖北）某厂用鲜牛奶在某台设备上生产两种奶制品．生产1吨A产品需鲜牛奶2吨，使用设备1小时，获利1000元；生产1吨B产品需鲜牛奶1.5吨，使用设备1.5小时，获利1200元．要求每天B产品的产量不超过A产品产量的2倍，设备每天生产两种产品时间之和不超过12小时. 假定每天可获取的鲜牛奶数量W（单位：吨）是一个随机变量，其分布列为

    （Ⅰ）求Z的分布列和均值；该厂每天根据获取的鲜牛奶数量安排生产，使其获利最大，因此每天的最大获利Z（单位：元）是一个随机变量．
    （Ⅱ） 若每天可获取的鲜牛奶数量相互独立，求3天中至少有1天的最大获利超过10000元的概率．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】盒中有6只灯泡，其中2只次品，4只正品，有放回地从中任取两次，每次取一只，试求下列事件的概率：
    （1）取到的2只都是次品；
    （2）取到的2只中正品、次品各一只；
    （3）取到的2只中至少有一只正品．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知过点的圆的圆心在轴的非负半轴上，且圆截直线所得弦长为．

    （1）求的标准方程；

    （2）若过点且斜率为的直线交圆于、两点，若的面积为，求直线的方程．

    查看答案和解析>>

    同步练习册答案