
【题目】四棱锥![]() 中,
中,![]() 面
面![]() ,底面
,底面![]() 是菱形,且
是菱形,且![]() ,
,![]() ,过点
,过点![]() 作直线
作直线![]() ,
,![]() 为直线
为直线![]() 上一动点.
上一动点.
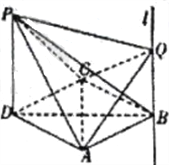
(1)求证:![]() ;
;
(2)当面![]() 面
面![]() 时,求三棱锥
时,求三棱锥![]() 的体积.
的体积.
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案科目:高中数学 来源: 题型:
【题目】5名男生4名女生站成一排,求满足下列条件的排法:
(1)女生都不相邻有多少种排法?
(2)男生甲、乙、丙排序一定(只考虑位置的前后顺序),有多少种排法?
(3)男甲不在首位,男乙不在末位,有多少种排法?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知一家公司生产某种品牌服装的年固定成本为![]() 万元,每生产
万元,每生产![]() 千件需另投入
千件需另投入![]() 万元.设该公司一年内共生产该品牌服装
万元.设该公司一年内共生产该品牌服装![]() 千件并全部销售完,每千件的销售收入为
千件并全部销售完,每千件的销售收入为![]() 万元,且
万元,且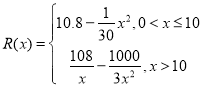 .
.
(1)写出年利润![]() (万元)关于年产量
(万元)关于年产量![]() (千件)的函数解析式;
(千件)的函数解析式;
(2)年产量为多少千件时,该公司在这一品牌服装的生产中所获得利润最大?(注:年利润=年销售收入-年总成本)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某中学为调查该校学生每周参加社会实践活动的情况,随机收集了若干名学生每周参加社会实践活动的时间(单位:小时),将样本数据绘制如图所示的频率分布直方图,且在[0,2)内的学生有1人.
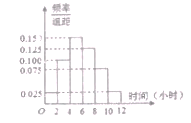
(1)求样本容量![]() ,并根据频率分布直方图估计该校学生每周参加社会实践活动时间的平均值;
,并根据频率分布直方图估计该校学生每周参加社会实践活动时间的平均值;
(2)将每周参加社会实践活动时间在[4,12]内定义为“经常参加社会实践”,参加活动时间在[0,4)内定义为“不经常参加社会实践”.已知样本中所有学生都参加了青少年科技创新大赛,有13人成绩等级为“优秀”,其余成绩为“一般”,其中成绩优秀的13人种“经常参加社会实践活动”的有12人.请将2×2列联表补充完整,并判断能否在犯错误的概率不超过0.05的前提下认为青少年科技创新大赛成绩“优秀”与经常参加社会实践活动有关;
(3)在(2)的条件下,如果从样本中“不经常参加社会实践”的学生中随机选取两人参加学校的科技创新班,求其中恰好一人成绩优秀的概率.
参考公式和数据:
![]() .
.
| 0.10 | 0.05 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
,![]() .
.
(1)若![]() ,判断函数
,判断函数![]() 的奇偶性,并加以证明;
的奇偶性,并加以证明;
(2)若函数![]() 在
在![]() 上是增函数,求实数
上是增函数,求实数![]() 的取值范围;
的取值范围;
(3)若存在实数![]() 使得关于
使得关于![]() 的方程
的方程![]() 有三个不相等的实数根,求实数
有三个不相等的实数根,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 的直角顶点
的直角顶点![]() 在
在![]() 轴上,点
轴上,点![]() 为斜边
为斜边![]() 的中点,且
的中点,且![]() 平行于
平行于![]() 轴.
轴.
(Ⅰ)求点![]() 的轨迹方程;
的轨迹方程;
(Ⅱ)设点![]() 的轨迹为曲线
的轨迹为曲线![]() ,直线
,直线![]() 与
与![]() 的另一个交点为
的另一个交点为![]() .以
.以![]() 为直径的圆交
为直径的圆交![]() 轴于
轴于![]() 即此圆的圆心为
即此圆的圆心为![]() ,
,![]() 求
求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某厂有4台大型机器,在一个月中,一台机器至多出现1次故障,且每台机器是否出现故障是相互独立的,出现故障时需1名工人进行维修,每台机器出现故障需要维修的概率为![]() .
.
(1)若出现故障的机器台数为![]() ,求
,求![]() 的分布列;
的分布列;
(2) 该厂至少有多少名工人才能保证每台机器在任何时刻同时出现故障时能及时进行维修的概率不少于90%?
(3)已知一名工人每月只有维修1台机器的能力,每月需支付给每位工人1万元的工资,每台机器不出现故障或出现故障能及时维修,就使该厂产生5万元的利润,否则将不产生利润,若该厂现有2名工人,求该厂每月获利的均值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,
, ![]() 为焦点是
为焦点是![]() 的抛物线上一点,
的抛物线上一点, ![]() 为直线
为直线![]() 上任一点,
上任一点, ![]() 分别为椭圆
分别为椭圆![]() 的上,下顶点,且
的上,下顶点,且![]() 三点的连线可以构成三角形.
三点的连线可以构成三角形.
(1)求椭圆![]() 的方程;
的方程;
(2)直线![]() 与椭圆
与椭圆![]() 的另一交点分别交于点
的另一交点分别交于点![]() ,求证:直线
,求证:直线![]() 过定点.
过定点.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com