
【题目】已知抛物线y=﹣ ![]() +bx+c与y轴交于点C,与x轴的两个交点分别为A(﹣4,0),B(1,0).
+bx+c与y轴交于点C,与x轴的两个交点分别为A(﹣4,0),B(1,0).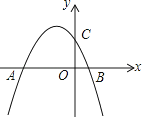
(1)求抛物线的解析式;
(2)已知点P在抛物线上,连接PC,PB,若△PBC是以BC为直角边的直角三角形,求点P的坐标;
(3)已知点E在x轴上,点F在抛物线上,是否存在以A,C,E,F为顶点的四边形是平行四边形?若存在,请直接写出点E的坐标;若不存在,请说明理由.
【答案】
(1)
解:抛物线的解析式为y=﹣ ![]() (x+4)(x﹣1),即y=﹣
(x+4)(x﹣1),即y=﹣ ![]() x2﹣
x2﹣ ![]() x+2;
x+2;
(2)
解:存在.
当x=0,y═﹣ ![]() x2﹣
x2﹣ ![]() x+2=2,则C(0,2),
x+2=2,则C(0,2),
∴OC=2,
∵A(﹣4,0),B(1,0),
∴OA=4,OB=1,AB=5,
当∠PCB=90°时,
∵AC2=42+22=20,BC2=22+12=5,AB2=52=25
∴AC2+BC2=AB2
∴△ACB是直角三角形,∠ACB=90°,
∴当点P与点A重合时,△PBC是以BC为直角边的直角三角形,此时P点坐标为(﹣4,0);
当∠PBC=90°时,PB∥AC,如图1,
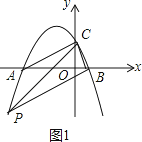
设直线AC的解析式为y=mx+n,
把A(﹣4,0),C(0,2)代入得 ![]() ,解得
,解得  ,
,
∴直线AC的解析式为y= ![]() x+2,
x+2,
∵BP∥AC,
∴直线BP的解析式为y= ![]() x+p,
x+p,
把B(1,0)代入得 ![]() +p=0,解得p=﹣
+p=0,解得p=﹣ ![]() ,
,
∴直线BP的解析式为y= ![]() x﹣
x﹣ ![]() ,
,
解方程组 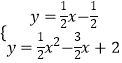 得
得 ![]() 或
或 ![]() ,此时P点坐标为(﹣5,﹣3);
,此时P点坐标为(﹣5,﹣3);
综上所述,满足条件的P点坐标为(﹣4,0),P2(﹣5,﹣3);
(3)
解:存在点E,设点E坐标为(m,0),F(n,﹣ ![]() n2﹣
n2﹣ ![]() n+2)
n+2)
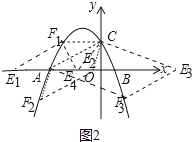
①当AC为边,CF1∥AE1,易知CF1=3,此时E1坐标(﹣7,0),
②当AC为边时,AC∥EF,易知点F纵坐标为﹣2,
∴﹣ ![]() n2﹣
n2﹣ ![]() n+2=﹣2,解得n=
n+2=﹣2,解得n= ![]() ,得到F2(
,得到F2( ![]() ,﹣2),F3(
,﹣2),F3( ![]() ,﹣2),
,﹣2),
根据中点坐标公式得到: ![]() =
= ![]() 或
或 ![]() =
= ![]() ,
,
解得m= ![]() 或
或 ![]() ,
,
此时E2( ![]() ,0),E3(
,0),E3( ![]() ,0),
,0),
③当AC为对角线时,AE4=CF1=3,此时E4(﹣1,0),
综上所述满足条件的点E为(﹣7,0)或(﹣1,0)或( ![]() ,﹣2)或(
,﹣2)或( ![]() ,﹣2).
,﹣2).
【解析】本题考查二次函数综合题、一次函数、勾股定理、平行四边形的判定和性质、中点坐标公式等知识,解题的关键是构建一次函数利用方程组解决点P坐标,学会分类讨论,学会用方程的思想解决问题,属于中考压轴题.
(1)因为抛物线经过点A(﹣4,0),B(1,0),所以可以设抛物线为y=﹣ ![]() (x+4)(x﹣1),展开即可解决问题;
(x+4)(x﹣1),展开即可解决问题;
(2)先证明∠ACB=90°,点A就是所求的点P,求出直线AC解析式,再求出过点B平行AC的直线的解析式,利用方程组即可解决问题;
(3)分AC为平行四边形的边,AC为平行四边形的对角线两种切线讨论即可解决问题.


 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案科目:高中数学 来源: 题型:
【题目】已知M是正四面体ABCD棱AB的中点,N是棱CD上异于端点C,D的任一点,则下列结论中,正确的个数有( )
(1)MN⊥AB;
(2)若N为中点,则MN与AD所成角为60°;
(3)平面CDM⊥平面ABN;
(4)不存在点N,使得过MN的平面与AC垂直.
A.1
B.2
C.3
D.4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知双曲线![]() 的焦点是椭圆
的焦点是椭圆![]() :
: ![]() (
(![]() )的顶点,且椭圆与双曲线的离心率互为倒数.
)的顶点,且椭圆与双曲线的离心率互为倒数.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)设动点![]() ,
, ![]() 在椭圆
在椭圆![]() 上,且
上,且![]() ,记直线
,记直线![]() 在
在![]() 轴上的截距为
轴上的截距为![]() ,求
,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在矩形![]() 中,
中,![]() 为
为![]() 的中点,
的中点,![]() 为线段
为线段![]() 上的一点,且
上的一点,且![]() .现将四边形
.现将四边形![]() 沿直线
沿直线![]() 翻折,使翻折后的二面角
翻折,使翻折后的二面角![]() 的余弦值为
的余弦值为![]() .
.
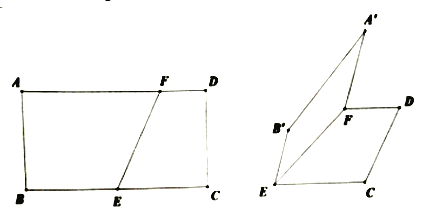
(1)求证:![]() ;
;
(2)求直线![]() 与平面
与平面![]() 所成角的大小.
所成角的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
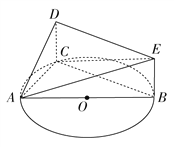
【题目】如图,AB是圆O的直径,点C在圆O上,矩形DCBE所在的平面垂直于圆O所在的平面, ![]() ,
, ![]() .
.
(1)若![]() ,求三棱锥
,求三棱锥![]() 的体积;
的体积;
(2)证明:平面ACD⊥平面BCDE;
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】阅读下列材料:
北京市正围绕着“政治中心、文化中心、国际交往中心、科技创新中心”的定位,深入实施“人文北京、科技北京、绿色北京”的发展战略.“十二五”期间,北京市文化创意产业展现了良好的发展基础和巨大的发展潜力,已经成为首都经济增长的支柱产业.
2011年,北京市文化创意产业实现增加值1938.6亿元,占地区生产总值的12.2%.2012年,北京市文化创意产业继续呈现平稳发展态势,实现产业增加值2189.2亿元,占地区生产总值的12.3%,是第三产业中仅次于金融业、批发和零售业的第三大支柱产业.2013年,北京市文化产业实现增加值2406.7亿元,比上年增长9.1%,文化创意产业作为北京市支柱产业已经排到了第二位.2014年,北京市文化创意产业实现增加值2749.3亿元,占地区生产总值的13.1%,创历史新高,2015年,北京市文化创意产业发展总体平稳,实现产业增加值3072.3亿元,占地区生产总值的13.4%.
根据以上材料解答下列问题:
(1)用折线图将2011﹣2015年北京市文化创意产业实现增加值表示出来,并在图中标明相应数据;
(2)根据绘制的折线图中提供的信息,预估2016年北京市文化创意产业实现增加值约亿元,你的预估理由 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com