
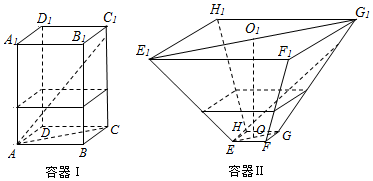
���� ��1���貣������CC1�ϵĵ�ΪM����������ˮ��Ľ���ΪN����N��NP��MC����AC�ڵ�P���Ƶ���CC1��ƽ��ABCD��CC1��AC��NP��AC�����MC=30cm���Ƶ�����ANP�ס�AMC���ɴ��ܳ�������lû��ˮ�в��ֵij��ȣ�
��2���貣������GG1�ϵĵ�ΪM����������ˮ��Ľ���ΪN������N��NP��EG����EG�ڵ�P������E��EQ��E1G1����E1G1�ڵ�Q���Ƶ���EE1G1GΪ�������Σ����E1Q=24cm��E1E=40cm�������Ҷ������sin��GEM=$\frac{3}{5}$���ɴ������������lû��ˮ�в��ֵij��ȣ�
��� �⣺��1���貣������CC1�ϵĵ�ΪM����������ˮ��Ľ���ΪN��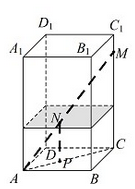
��ƽ��ACM�У���N��NP��MC����AC�ڵ�P��
��ABCD-A1B1C1D1Ϊ������������CC1��ƽ��ABCD��
�֡�AC?ƽ��ABCD����CC1��AC����NP��AC��
��NP=12cm����AM2=AC2+MC2�����MC=30cm��
��NP��MC�����ANP�ס�AMC��
��$\frac{AN}{AM}$=$\frac{NP}{MC}$��$\frac{AN}{40}=\frac{12}{30}$����AN=16cm��
�ಣ����lû��ˮ�в��ֵij���Ϊ16cm��
��2���貣������GG1�ϵĵ�ΪM����������ˮ��Ľ���ΪN��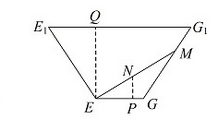
��ƽ��E1EGG1�У�����N��NP��EG����EG�ڵ�P��
����E��EQ��E1G1����E1G1�ڵ�Q��
��EFGH-E1F1G1H1Ϊ������̨����EE1=GG1��EG��E1G1��
EG��E1G1��
��EE1G1GΪ�������Σ�����ƽ��E1EGG1��ƽ��ͼ��
��E1G1=62cm��EG=14cm��EQ=32cm��NP=12cm��
��E1Q=24cm��
�ɹ��ɶ����ã�E1E=40cm��
��sin��EE1G1=$\frac{4}{5}$��sin��EGM=sin��EE1G1=$\frac{4}{5}$��cos$��EGM=-\frac{3}{5}$��
�������Ҷ����ã�$\frac{EM}{sin��EGM}$=$\frac{EG}{sin��EMG}$����sin$��EMG=\frac{7}{25}$��cos$��EMG=\frac{24}{25}$��
��sin��GEM=sin����EGM+��EMG��=sin��EGMcos��EMG+cos��EGMsin��EMG=$\frac{3}{5}$��
��EN=$\frac{NP}{sin��GEM}$=$\frac{12}{\frac{3}{5}}$=20cm��
�ಣ����lû��ˮ�в��ֵij���Ϊ20cm��
���� ���⿼�鲣����lû��ˮ�в��ֵij��ȵ�������ռ������ߡ����桢������λ�ù�ϵ�Ȼ���֪ʶ������������֤��������������������ռ������������������ν��˼�롢������ת��˼�룬���е��⣮


 ȫ�ܲ��һ���þ�ϵ�д�
ȫ�ܲ��һ���þ�ϵ�д� ��ɢ˼ά�¿���ϵ�д�
��ɢ˼ά�¿���ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | �٢� | B�� | �٢� | C�� | �ۢ� | D�� | �ڢ� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 3 | B�� | 2$\sqrt{2}$ | C�� | $\sqrt{5}$ | D�� | 2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
| 1 | 2 | 3 | �� | m+n |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 16 | B�� | 14 | C�� | 12 | D�� | 10 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{6}{5}$ | B�� | 1 | C�� | $\frac{3}{5}$ | D�� | $\frac{1}{5}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com