
| 1 | 2 | 3 | … | m+n |
分析 (1)设事件Ai表示编号为i的抽屉里放的是黑球,则p=p(A2)=P(A2|A1)P(A1)+P(A2|$\overline{{A}_{1}}$)P($\overline{{A}_{1}}$),由此能求出编号为2的抽屉内放的是黑球的概率.
(2)X的所有可能取值为$\frac{1}{n},\frac{1}{n+1}$,…,$\frac{1}{n+m}$,P(x=$\frac{1}{k}$)=$\frac{{C}_{k-1}^{n-1}}{{C}_{m+n}^{n}}$,k=n,n+1,n+2,…,n+m,从而E(X)=$\sum_{k=1}^{n+m}$($\frac{1}{k}•\frac{{C}_{k-1}^{n-1}}{{C}_{n+m}^{n}}$)=$\frac{1}{{C}_{n+m}^{n}}•\sum_{k=n}^{n+m}\frac{{C}_{k-1}^{n-1}}{k}$,由此能证明E(X)<$\frac{n}{(m+n)(n-1)}$.
解答 解:(1)设事件Ai表示编号为i的抽屉里放的是黑球,
则p=p(A2)=P(A2|A1)P(A1)+P(A2|$\overline{{A}_{1}}$)P($\overline{{A}_{1}}$)
=$\frac{n-1}{m+n-1}×\frac{n}{m+n}+\frac{n}{m+n-1}×\frac{m}{m+n}$
=$\frac{{n}^{2}-n+mn}{(m+n)(m+n-1)}$=$\frac{n}{m+n}$.
证明:(2)∵X的所有可能取值为$\frac{1}{n},\frac{1}{n+1}$,…,$\frac{1}{n+m}$,
P(x=$\frac{1}{k}$)=$\frac{{C}_{k-1}^{n-1}}{{C}_{m+n}^{n}}$,k=n,n+1,n+2,…,n+m,
∴E(X)=$\sum_{k=1}^{n+m}$($\frac{1}{k}•\frac{{C}_{k-1}^{n-1}}{{C}_{n+m}^{n}}$)=$\frac{1}{{C}_{n+m}^{n}}•\sum_{k=n}^{n+m}\frac{{C}_{k-1}^{n-1}}{k}$
=$\frac{1}{{C}_{n+m}^{n}}•\sum_{k=n}^{n+m}\frac{{C}_{k-1}^{n-1}}{k}$<$\frac{1}{{C}_{n+m}^{n}}•\sum_{k=n}^{n+m}\frac{{C}_{k-1}^{n-1}}{k-1}$=$\frac{1}{{C}_{n+m}^{n}}•\sum_{k=n}^{n+m}\frac{{C}_{k-2}^{n-2}}{n-1}$
=$\frac{1}{(n-1){C}_{n+m}^{n}}$•(${C}_{n-2}^{n-2}+{C}_{n-1}^{n-2}+…+{C}_{n+m-2}^{n-2}$)
=$\frac{1}{(n-1){C}_{m+n}^{n}}•{C}_{m+n-1}^{n-1}$=$\frac{n}{(m+n)(n-1)}$,
∴E(X)<$\frac{n}{(m+n)(n-1)}$.
点评 本题考查概率的求法,考查离散型随机变量的分布列、数学期望等基础知识,考查推理论证能力、运算求解能力、空间想象能力,考查数形结合思想、化归与转化思想,是中档题.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 最高气温 | [10,15) | [15,20) | [20,25) | [25,30) | [30,35) | [35,40) |
| 天数 | 2 | 16 | 36 | 25 | 7 | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
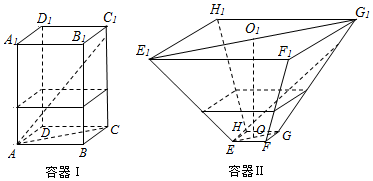
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
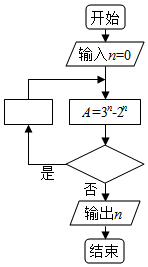 如图程序框图是为了求出满足3n-2n>1000的最小偶数n,那么在
如图程序框图是为了求出满足3n-2n>1000的最小偶数n,那么在 和
和 两个空白框中,可以分别填入( )
两个空白框中,可以分别填入( )| A. | A>1000和n=n+1 | B. | A>1000和n=n+2 | C. | A≤1000和n=n+1 | D. | A≤1000和n=n+2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 最高气温 | [10,15) | [15,20) | [20,25) | [25,30) | [30,35) | [35,40) |
| 天数 | 2 | 16 | 36 | 25 | 7 | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com