
分析 由向量的平方即为模的平方,化简整理可得x2$\overrightarrow{a}$2+2x$\overrightarrow{a}$•$\overrightarrow{b}$+$\overrightarrow{a}$•$\overrightarrow{b}$-$\frac{1}{4}$$\overrightarrow{a}$2≥0恒成立,可得4($\overrightarrow{a}$•$\overrightarrow{b}$)2-4$\overrightarrow{a}$2•($\overrightarrow{a}$•$\overrightarrow{b}$-$\frac{1}{4}$$\overrightarrow{a}$2)≤0,(θ为$\overrightarrow{a}$,$\overrightarrow{b}$的夹角),即有(cosθ-$\frac{1}{2}$)2≤0,可得cosθ=$\frac{1}{2}$,sinθ=$\frac{\sqrt{3}}{2}$,可设|$\overrightarrow{a}$|=|$\overrightarrow{b}$|=2,|$\overrightarrow{c}$|=1,设$\overrightarrow{OA}$=$\overrightarrow{a}$=(2,0),$\overrightarrow{OB}$=$\overrightarrow{b}$=(1,$\sqrt{3}$),$\overrightarrow{OC}$=$\overrightarrow{c}$,C在单位圆上运动,由$\overrightarrow{OP}$=λ$\overrightarrow{a}$+(1-λ)$\overrightarrow{b}$可得P在线段AB上运动(不含端点),求出AB的方程,运用点到直线的距离公式可得O到AB的距离,即可得到所求最值和范围.
解答  解:对任意的x∈R,都有|$\overrightarrow{b}$+x$\overrightarrow{a}$|≥|$\overrightarrow{b}$-$\frac{1}{2}$$\overrightarrow{a}$|,
解:对任意的x∈R,都有|$\overrightarrow{b}$+x$\overrightarrow{a}$|≥|$\overrightarrow{b}$-$\frac{1}{2}$$\overrightarrow{a}$|,
即有($\overrightarrow{b}$+x$\overrightarrow{a}$)2≥($\overrightarrow{b}$-$\frac{1}{2}$$\overrightarrow{a}$)2,
即为$\overrightarrow{b}$2+2x$\overrightarrow{a}$•$\overrightarrow{b}$+x2$\overrightarrow{a}$2≥$\overrightarrow{b}$2-$\overrightarrow{a}$•$\overrightarrow{b}$+$\frac{1}{4}$$\overrightarrow{a}$2,
由|$\overrightarrow{a}$|=|$\overrightarrow{b}$|,可得x2$\overrightarrow{a}$2+2x$\overrightarrow{a}$•$\overrightarrow{b}$+$\overrightarrow{a}$•$\overrightarrow{b}$-$\frac{1}{4}$$\overrightarrow{a}$2≥0恒成立,
可得4($\overrightarrow{a}$•$\overrightarrow{b}$)2-4$\overrightarrow{a}$2•($\overrightarrow{a}$•$\overrightarrow{b}$-$\frac{1}{4}$$\overrightarrow{a}$2)≤0,(θ为$\overrightarrow{a}$,$\overrightarrow{b}$的夹角),
即为|$\overrightarrow{a}$|4•cos2θ-|$\overrightarrow{a}$|4•cosθ+$\frac{1}{4}$|$\overrightarrow{a}$|4≤0,
即有(cosθ-$\frac{1}{2}$)2≤0,(cosθ-$\frac{1}{2}$)2≥0,
可得cosθ=$\frac{1}{2}$,sinθ=$\frac{\sqrt{3}}{2}$,
可设|$\overrightarrow{a}$|=|$\overrightarrow{b}$|=2,|$\overrightarrow{c}$|=1,
设$\overrightarrow{OA}$=$\overrightarrow{a}$=(2,0),$\overrightarrow{OB}$=$\overrightarrow{b}$=(1,$\sqrt{3}$),
$\overrightarrow{OC}$=$\overrightarrow{c}$,C在单位圆上运动,
由$\overrightarrow{OP}$=λ$\overrightarrow{a}$+(1-λ)$\overrightarrow{b}$可得P在线段AB上运动(不含端点),
直线AB的方程为y-0=-$\sqrt{3}$(x-2),
即为$\sqrt{3}$x+y-2$\sqrt{3}$=0.
由原点到直线AB的距离为$\frac{|0+0-2\sqrt{3}|}{\sqrt{3+1}}$=$\sqrt{3}$,
即有单位圆上的点到线段AB的距离的最小值为$\sqrt{3}$-1,最大值为$\sqrt{3}$+1,
则$\frac{|\overrightarrow{c}-λ\overrightarrow{a}-(1-λ)\overrightarrow{b}|}{|\overrightarrow{a}|}$=$\frac{|\overrightarrow{OC}-\overrightarrow{OP}|}{2}$的范围是[$\frac{1}{2}$($\sqrt{3}$-1),$\frac{1}{2}$($\sqrt{3}$+1)].
故答案为:[$\frac{1}{2}$($\sqrt{3}$-1),$\frac{1}{2}$($\sqrt{3}$+1)].
点评 本题考查向量数量积的运用,注意运用性质:向量的平方即为模的平方,考查恒成立思想转化为二次不等式恒成立问题的解法,以及数形结合的思想方法,考查化简整理的运算能力,属于难题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ①② | B. | ①③ | C. | ③④ | D. | ②④ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{4}$ | B. | $\frac{π}{3}$ | C. | $\frac{2π}{3}$ | D. | $\frac{3π}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
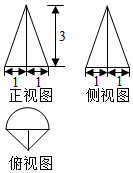 某几何体的三视图如图所示(单位:cm),则该几何体的体积(单位:cm2)是( )
某几何体的三视图如图所示(单位:cm),则该几何体的体积(单位:cm2)是( )| A. | $\frac{π}{2}$+1 | B. | $\frac{π}{2}$+3 | C. | $\frac{3π}{2}$+1 | D. | $\frac{3π}{2}$+3 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 1 | 2 | 3 | … | m+n |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com