练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    3．已知抛物线C：y2=2px的焦点与圆x2+y2-2x-15=0的圆心重合，则抛物线C的方程是（　　）
    A．y2=2xB．y2=-2xC．y2=4xD．y2=-4x

    分析 求出圆的圆心坐标，然后求解抛物线方程．

    解答 解：圆x2+y2-2x-15=0的圆心（1，0），抛物线C：y2=2px的焦点与圆x2+y2-2x-15=0的圆心重合，
    可得：p=2，所求抛物线方程为：y2=4x．
    故选：C．

    点评 本题考查圆的方程的应用以及抛物线方程的求法，考查转化思想以及计算能力．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    13．我国古代有着辉煌的数学研究成果．《周髀算经》、《九章算术》、《海岛算经》、《孙子算经》、…、《辑古算经》等算经10部专著，有着十分丰富多彩的内容，是了解我国古代数学的重要文献．这10部专著中有7部产生于魏晋南北朝时期．某中学拟从这10部名著中选择2部作为“数学文化”校本课程学习内容，则所选2部名著中至少有一部是魏晋南北朝时期的名著的概率为（　　）
    A．$\frac{14}{15}$B．$\frac{13}{15}$C．$\frac{2}{9}$D．$\frac{7}{9}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

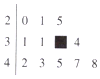    14．在如图所示一组数据的茎叶图中，有一个数字被污染后而模糊不清，但曾计算得该组数据的极差与中位数之和为61，则被污染的数字为（　　）
    A．1B．2C．3D．4

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

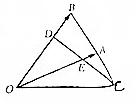    11．在△ABO中，点C是点B关于点A的对称点，点D是OB靠近B的三等分点，DC与OA交于E点，设$\overrightarrow{OA}$=$\overrightarrow{a}$，$\overrightarrow{OB}$=$\overrightarrow{b}$，用$\overrightarrow{a}$，$\overrightarrow{b}$表示$\overrightarrow{OC}$，$\overrightarrow{CD}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

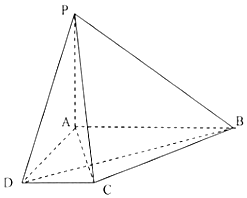    18．如图，四棱锥P-ABCD中，底面ABCD为直角梯形，∠BAD=∠ADC=90°，AP=AD=2CD=1，AB=2，PA⊥平面ABCD．
    （1）求证：平面PBD⊥平面PAC；
    （2）若侧棱PB上存在点Q，使得VP-ACD：VQ-ABC=1：2，求二面角Q-AC-B的余弦值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    8．如图1为正方形ABCD的边长为2，AC∩BD=O，将正方形ABCD沿对角线BD折起，使AC=a，得到三棱锥A-BCD（如图2）
    （1）点E在棱AB上，且AE=3EB，点F在棱AC上，且AF=2FC，求证：DF∥平面CED
    （2）当a为何值时，三棱锥A-BCD的体积最大？并求出最大值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    15．设Sn为各项不相等的等差数列an的前n 项和，已知a3a8=3a11，S3=9．
    （1）求数列{an}的通项公式；
    （2）若bn=$\frac{1}{\sqrt{{a}_{n}}+\sqrt{{a}_{n+1}}}$，数列{bn}的前n 项和为Tn，求$\frac{{a}_{n+1}}{{T}_{n}}$的最小值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    12．已知过原点的直线l与圆C：x2+y2-6x+5=0相交于不同的两点A、B，且线段AB中点坐标为（2，$\sqrt{2}$），则弦长为（　　）
    A．2B．3C．4D．5

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    13．甲、乙两企业根据赛事组委会要求为获奖者定做某工艺品作为奖品，其中一等奖奖品3件，二等奖奖品6件；制作一等奖、二等奖所用原料完全相同，但工艺不同，故价格有所差异．甲厂收费便宜，但原料有限，最多只能制作4件奖品，乙厂原料充足，但收费较贵，其具体收费如表所示，则组委会定做该工艺品的费用总和最低为4900元．
    奖品
    缴费（无/件）
    工厂    		一等奖奖品二等奖奖品
    甲500400
    乙800600

    查看答案和解析>>

    同步练习册答案