
| t(时) | 0 | 3 | 6 | 9 | 12 | 15 | 18 | 21 | 24 |
| y(米) | 1.5 | 2.4 | 1.5 | 0.6 | 1.4 | 2.4 | 1.6 | 0.6 | 1.5 |
分析 (Ⅰ)根据表中近似数据画出散点图,选②y=Acos(ωt+ϕ)+b做为函数模型,由此利用三角函数的图象和性质能求出该拟合模型的函数解析式.
(Ⅱ)由$y=0.9sin(\frac{π}{6}t)+1.5$,令y≥1.05,得$sin(\frac{π}{6}t)≥-\frac{1}{2}$,从而12k-1≤t≤12k+7,由此能求出这一天可以安排早上5点至7点以及11点至18点的时间段组织训练,才能确保集训队员的安全.
解答 (满分12分)
解:(Ⅰ)根据表中近似数据画出散点图,如图所示: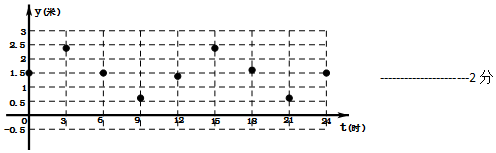
依题意,选②y=Acos(ωt+ϕ)+b做为函数模型,
∴$A=\frac{2.4-0.6}{2}=0.9b=\frac{2.4+0.6}{2}=1.5$,
∵$T=\frac{2π}{ω}=12∴ω=\frac{π}{6}$∴$y=0.9cos(\frac{π}{6}t+φ)+1.5$-------------------------------------------------------------(5分)
又∵函数y=0.9cos($\frac{π}{6}t+$φ)+1.5的图象过点(3,2.4),
∴2.4=0.9×cos($\frac{π}{6}×3$+φ)+1.5,
∴cos($\frac{π}{2}$+φ)=1,∴sinφ=-1,
又∵-π<φ<0,∴φ=-$\frac{π}{2}$,
∴$y=0.9cos(\frac{π}{6}t-\frac{π}{2})+1.5=0.9sin(\frac{π}{6}t)+1.5$------------------------------------(7分)
(Ⅱ)由(Ⅰ)知:$y=0.9sin(\frac{π}{6}t)+1.5$
令y≥1.05,即$0.9sin(\frac{π}{6}t)+1.5≥1.05$∴$sin(\frac{π}{6}t)≥-\frac{1}{2}$--------------------------------------------------------------------------------(9分)
∴$2kπ-\frac{π}{6}≤\frac{π}{6}t≤2kπ+\frac{7π}{6}(k∈Z)$,
∴12k-1≤t≤12k+7
又∵5≤t≤18∵5≤t≤7或11≤t≤18-----------------------------------------------------------------------(11分)
∴这一天可以安排早上5点至7点以及11点至18点的时间段组织训练,
才能确保集训队员的安全.-----------------------------------------------------------------(12分)
点评 本题考查函数解析式的求法,考查确保集训队员的安全的训练时间的确定,考查三角函数的图象与性质等基础知识,考查化归与转化思想,数形结合思想,是中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| x(万元) | 2 | 4 | 5 | 6 | 8 |
| y(万元) | 28 | 36 | 52 | 56 | 78 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 29 | B. | 21 | C. | 19 | D. | 17 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com