
分析 利用$\overrightarrow{O{A}^{′}}$=$\overrightarrow{OA}+\overrightarrow{a}$=(3,4),同理可得$\overrightarrow{OB′}$,$\overrightarrow{OC′}$.
解答 解:$\overrightarrow{O{A}^{′}}$=$\overrightarrow{OA}+\overrightarrow{a}$=(3,4),
同理可得$\overrightarrow{OB′}$=(1,2),$\overrightarrow{OC′}$=(7,0).
∴$\overrightarrow{OA′}$+$\overrightarrow{OB′}$+$\overrightarrow{OC′}$=(3,4)+(1,2)+(7,0)=(11,6).
点评 本题考查了向量的三角形法则,考查了推理能力与计算能力,属于基础题.


 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案 出彩同步大试卷系列答案
出彩同步大试卷系列答案科目:高中数学 来源: 题型:解答题
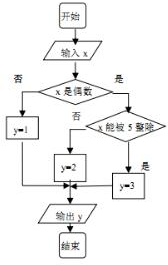 某算法的程序图如图所示,其中输入的变量x在1,2,3,…,30这30个整数中等可能随机产生.
某算法的程序图如图所示,其中输入的变量x在1,2,3,…,30这30个整数中等可能随机产生.| 运行次数 | 输出y=1的频数 | 输出y=2的频数 | 输出y=3的频数 |
| 50 | 24 | 19 | 7 |
| … | … | … | … |
| 2000 | 1027 | 776 | 197 |
| 运行次数 | 输出y=1的频数 | 输出y=2的频数 | 输出y=3的频数 |
| 50 | 26 | 11 | 13 |
| … | … | … | … |
| 2000 | 1051 | 396 | 553 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 45° | B. | 15° | C. | 105° | D. | 165° |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (¬p)∨(¬q) | B. | (¬p)∧(¬q) | C. | (¬p)∧q | D. | p∧q |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com