
求证:(![]() ≥8.
≥8.
分析:这是一个条件不等式的证明问题,要注意观察不等式的结构特点和条件a+b+c=1的合理应用.可用综合法和分析法两种方法证明.
证法一:(综合法)
(![]() -1)(
-1)(![]() -1)(
-1)(![]() -1)
-1)
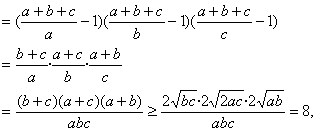
当且仅当a=b=c时取等号,所以不等式成立.
证法二:(分析法)
要证(![]() -1)(
-1)(![]() -1)(
-1)(![]() -1)≥8成立,
-1)≥8成立,
只需证![]() ≥8成立.
≥8成立.
因为a+b+c=1,
所以只需证![]() ≥8成立,
≥8成立,
即![]() ≥8.
≥8.
只需证![]() ≥8成立.
≥8成立.
而![]() ≥8显然成立,
≥8显然成立,
∴![]() ≥8成立.
≥8成立.
绿色通道:
综合法是从已知条件出发,经过逐步推理,最后达到待证的结论;而在分析法中,从结论出发的每一个步骤所得到的判断都是使结论成立的充分条件,最后一步归结到已被证明了的事实或已知.
在证明不等式时要注意应用重要不等式和不等式的性质,要注意基本不等式应用的条件及等号成立的条件.


科目:高中数学 来源: 题型:
| 1 | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 |
| 3 |
| 1 |
| a |
| 1 |
| b |
| 1 |
| c |
| a |
| b |
| c |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com