Question

【题目】若点（p，q），在|p|≤3，|q|≤3中按均匀分布出现．
（1）点M（x，y）横、纵坐标分别由掷骰子确定，第一次确定横坐标，第二次确定纵坐标，则点M（x，y）落在上述区域的概率？
（2）试求方程x2+2px﹣q2+1=0有两个实数根的概率．

Answer 1

【答案】
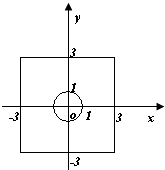
（1）解：根据题意，点（p，q），在|p|≤3，|q|≤3中，即在如图的正方形区域，

其中p、q都是整数的点有6×6=36个，

点M（x，y）横、纵坐标分别由掷骰子确定，即x、y都是整数，且1≤x≤3，1≤y≤3，

点M（x，y）落在上述区域有（1，1），（1，2），（1，3），（2，1），（2，2），（2，3），（3，1），（3，2），（3，3），有9个点，

所以点M（x，y）落在上述区域的概率P1=

（2）解：|p|≤3，|q|≤3表示如图的正方形区域，易得其面积为36；

若方程x2+2px﹣q2+1=0有两个实数根，则有△=（2p）2﹣4（﹣q2+1）≥0，

解可得p2+q2≥1，为如图所示正方形中圆以外的区域，其面积为36﹣π，

即方程x2+2px﹣q2+1=0有两个实数根的概率，P2= ．

【解析】（1）是古典概型，首先分析可得|p|≤3，|q|≤3整点的个数，进而分析可得点M的纵横坐标的范围，可得M的个数，由古典概型公式，计算可得答案；（2）是几何概型，首先可得|p|≤3，|q|≤3表示正方形区域，易得其面积，进而根据方程x2+2px﹣q2+1=0有两个实数根，则有△=（2p）2﹣4（﹣q2+1）≥0，变形可得p2+q2≥1，分析可得其表示的区域即面积，由几何概型公式，计算可得答案．
【考点精析】根据题目的已知条件，利用几何概型的相关知识可以得到问题的答案，需要掌握几何概型的特点：1）试验中所有可能出现的结果（基本事件）有无限多个；2）每个基本事件出现的可能性相等．