
【题目】如图所示, ![]() 是边长为
是边长为![]() 的正三角形,
的正三角形, ![]() 平面
平面![]() ,且
,且![]() 在平面
在平面![]() 的同侧,它们在
的同侧,它们在![]() 内的正射影分别是
内的正射影分别是![]() ,且
,且![]() 是
是![]() ,
, ![]() 到
到![]() 的距离为
的距离为![]() .
.
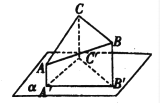
(1)求点![]() 到平面
到平面![]() 的距离;
的距离;
(2)求平面![]() 与平面
与平面![]() 所成锐二面角的余弦值.
所成锐二面角的余弦值.
 特高级教师点拨系列答案
特高级教师点拨系列答案科目:高中数学 来源: 题型:
【题目】某学校为推行“高效课堂”教学法,某数学老师分别用传统教学和“高效课堂”两种不同的教学方法,在同一年级的甲、乙两个同层次的班进行教学实验,为了解教学效果,期末考试后, 分别从两个班级中各随机抽取20名学生的成绩进行统计,作出的茎叶图如图(记成绩不低于70分者为“成绩优良”).
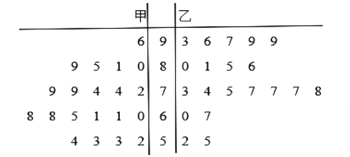
(1)分别计算甲、乙两班20个样本中,数学成绩前十名的平均分,并大致判断那种教学方法的教学效果更佳;
(2)由以上统计数据填写下面![]() 列联表,并判断能否在犯错误的概率不超过0.05的前提下认为“成绩优良与教学方法有关”?
列联表,并判断能否在犯错误的概率不超过0.05的前提下认为“成绩优良与教学方法有关”?

附: 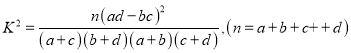
独立性检验临界表:

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分为14分)已知定义域为R的函数![]() 是奇函数.
是奇函数.
(1)求a,b的值;
(2)若对任意的t∈R,不等式f(t2-2t)+f(2t2-k)<0恒成立,求k的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙两人为了响应政府“节能减排”的号召,决定各购置一辆纯电动汽车.经了解目前市场上销售的主流纯电动汽车,按续驶里程数![]() (单位:公里)可分为三类车型,
(单位:公里)可分为三类车型, ![]() ,
, ![]() .甲从
.甲从![]() 三类车型中挑选,乙从
三类车型中挑选,乙从![]() 两类车型中挑选,甲、乙两人选择各类车型的概率如表:
两类车型中挑选,甲、乙两人选择各类车型的概率如表:
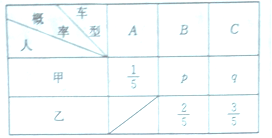
已知甲、乙都选![]() 类型的概率为
类型的概率为![]() .
.
(1)求![]() 的值;
的值;
(2)求甲、乙选择不同车型的概率;
(3)某市对购买纯电动汽车进行补贴,补贴标准如下表:

记甲、乙两人购车所获得的财政补贴之和为![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
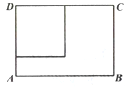
【题目】现有一张长为![]() ,宽为
,宽为![]() (
(![]() )的长方形铁皮
)的长方形铁皮![]() ,准备用它做成一个无盖长方体铁皮容器,要求材料利用率为100%,不考虑焊接处损失.如图,在长方形
,准备用它做成一个无盖长方体铁皮容器,要求材料利用率为100%,不考虑焊接处损失.如图,在长方形![]() 的一个角上剪下一块边长为
的一个角上剪下一块边长为![]() 的正方形铁皮,作为铁皮容器的底面,用余下材料剪拼后作为铁皮容器的侧面,设长方体的高为
的正方形铁皮,作为铁皮容器的底面,用余下材料剪拼后作为铁皮容器的侧面,设长方体的高为![]() ,体积为
,体积为![]() .
.
(Ⅰ)求![]() 关于
关于![]() 的函数关系式;
的函数关系式;
(Ⅱ)求该铁皮容器体积![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
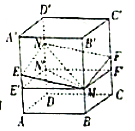
【题目】如图所示,正方体![]() 的棱长为1,
的棱长为1, ![]() ,
, ![]() 分别是棱
分别是棱![]() ,
, ![]() 的中点,过直线
的中点,过直线![]() 的平面分别与棱
的平面分别与棱![]() ,
, ![]() 交于
交于![]() ,
, ![]() ,设
,设![]() ,
, ![]() ,给出以下命题:
,给出以下命题:
①四边形![]() 为平行四边形;
为平行四边形;
②若四边形![]() 面积
面积![]() ,
, ![]() ,则
,则![]() 有最小值;
有最小值;
③若四棱锥![]() 的体积
的体积![]() ,
, ![]() ,则
,则![]() 为常函数;
为常函数;
④若多面体![]() 的体积
的体积![]() ,
, ![]() ,则
,则![]() 为单调函数.
为单调函数.
⑤当![]() 时,四边形
时,四边形![]() 为正方形.
为正方形.
其中假命题的个数为( )
A. 0 B. 3 C. 2 D. 1
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某届奥运会上,中国队以26金18银26铜的成绩称金牌榜第三、奖牌榜第二,某校体育爱好者在高三 年级一班至六班进行了“本届奥运会中国队表现”的满意度调查(结果只有“满意”和“不满意”两种),从被调查的学生中随机抽取了50人,具体的调查结果如下表:

(1)在高三年级全体学生中随机抽取一名学生,由以上统计数据估计该生持满意态度的概率;
(2)若从一班至二班的调查对象中随机选取4人进行追踪调查,记选中的4人中对“本届奥运会中国队表现”不满意的人数为![]() ,求随机变量
,求随机变量![]() 的分布列及数学期望.
的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】空气污染,又称为大气污染,是指由于人类活动或自然过程引起某些物质进入大气中,呈现出足够的浓度,达到足够的时间,并因此危害了人体的舒适、健康和福利或环境的现象.全世界也越来越关注环境保护问题.当空气污染指数(单位:μg/m3)为0~50时,空气质量级别为一级,空气质量状况属于优;当空气污染指数为50~100时,空气质量级别为二级,空气质量状况属于良;当空气污染指数为100~150时,空气质量级别为三级,空气质量状况属于轻度污染;当空气污染指数为150~200时,空气质量级别为四级,空气质量状况属于中度污染;当空气污染指数为200~300时,空气质量级别为五级,空气质量状况属于重度污染;当空气污染指数为300以上时,空气质量级别为六级,空气质量状况属于严重污染.2017年1月某日某省x个监测点数据统计如下:
空气污染指数 (单位:μg/m3) |
|
|
|
|
监测点个数 | 15 | 40 | y | 10 |
(1)根据所给统计表和频率分布直方图中的信息求出x,y的值,并完成频率分布直方图;
(2)若A市共有5个监测点,其中有3个监测点为轻度污染,2个监测点为良.从中任意选取2个监测点,事件A“其中至少有一个为良”发生的概率是多少?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com